Hvað er vedísk stærðfræði/reikningur og er hún kennd hér á landi?Vedísk stærðfræði getur þýtt tvennt: Annars vegar var stærðfræði, sem iðkuð var á Indlandi á svonefndu vedísku tímabili frá því um 1500 til um 500 – 400 fyrir Krist, nefnd vedísk stærðfræði. Indversk stærðfræði frá fornöld og miðöldum var samin á sanskrít og sett fram í þjöppuðu formi, ljóðum sem nefndust sūtra. Þá var hægara að muna textann. Þeim fylgdi texti í óbundnu máli með útlistunum og rökstuðningi. Talið er að um 600 fyrir Krist hafi ljóðin fengið það form sem nú er þekkt þótt ritaðar heimildir séu mun yngri. Í einu meginverkinu frá þessu tímabili, Baudhayana Sulba Sutra, er að finna dæmi um pýþagórískar þrenndir, svo sem (3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25) og (12, 35, 37). Einnig var þar að finna nálgunargildi fyrir ferningsrótina af 2: \[\sqrt{2}\approx1+\frac{1}{3}+\frac{1}{3\cdot4}-\frac{1}{3\cdot4\cdot34}=1.4142156...\] sem hefur fimm rétta aukastafi. Indverjar fundu einnig nálgun fyrir pí, 3,0883, í viðleitni til að finna hring með sama flatarmáli og gefinn ferningur (Katz, 1993). Hins vegar getur vedísk stærðfræði þýtt stærðfræðikerfi sem indverski stærðfræðingurinn Jagadguru Shri Bharathi Krishna Tirthaji setti fram á árunum 1911 til 1918 og birti í bókinni Vedic Mathematics Book. Vedísk stærðfræði er þar sett fram í sextán formúlum, Sutrum, og þrettán undirformúlum, Undir-Sutrum, sem nota má við dæmi úr reikningi, algebru, rúmfræði og fleiri sviðum stærðfræði. Aðferðirnar eru um að leysa viðfangsefni sem krefjast nokkurrar vinnu að leysa með hefðbundnum hætti. Dæmi um vedíska stærðfræði er verkefnið að margfalda saman 998 og 994 með aðferðinni Nikhilam Sutra: Báðar tölur eru dregnar frá 1000: \[1000-998=2\] \[1000-994=6\] \[2+6=8\] \[998–6=992\] \[994–2=992\] \[2·6=12\] Svarið er: \[998\cdot994=992.012\] Með algebrulegri aðferð má skýra aðferðina þannig: \[998\cdot994=(1.000–2)(1.000–6)\] \[=1.000\cdot1.000–2\cdot1000–6\cdot1000+2\cdot6\] \[=1.000.000–(2+6)\cdot1.000+2\cdot6\] \[=1.000.000–8.000+12\] \[=992.012 \] Fleiri slík dæmi um margföldun má skýra með algebrulegum aðferðum en Nikhilam Sutra er talin vera einfaldasta Sutra-aðferðin. Henni er beitt þegar tölurnar sem margfalda skal saman eru nálægt heilu veldi af tíu en einnig mætti velja aðra tölu, til dæmis 60. Í Nikhilam Sutra má þekkja skyldleika við gamlan húsgang. Í handritaðri íslenskri reikningsbók frá 1721, Arithmetica – Það er reikningslist, varðveittri í handritinu ÍB 217 4to, er kynnt hliðstæð aðferð til að margfalda saman tvær eins stafs tölur og skal summa þeirra vera hærri en tugur. Þá er hvor talan um sig dregin frá 10. Annar hvor mismunurinn er dreginn frá hinni upprunalegu tölunni til að fá tölustafinn í tugasætinu. Mismunirnir eru svo margfaldaðir saman til að fá töluna í einingasætinu. Dæmi er tekið af \[8\cdot7=56\]
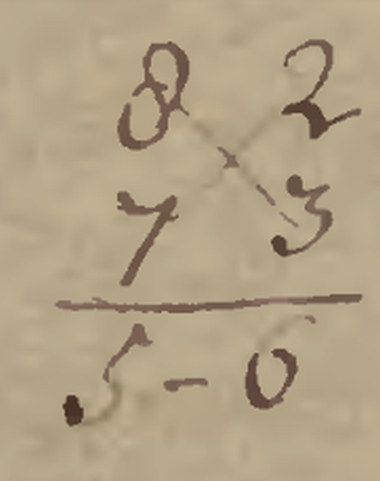
Hvor talan um sig dregin frá 10. Annar hvor mismunurinn er dreginn frá hinni upprunalegu tölunni til að fá tölustafinn í tugasætinu. Mismunirnir eru svo margfaldaðir saman til að fá töluna í einingasætinu.
| 782 | 19083 | |||||
| - | 336 | - | 1631 | |||
| 454 | (2 dregnir frá 6, svarið 4 yfirstrikað) | 18652 | (0 dregið frá 6, svarið 6 yfirstrikað) | |||
| = | 446 | = | 17452 |
- Katz, Victor (1993). A history of mathematics. An introduction. New York: Harper Collins College Publisher.
- Mathlearnes.com. What is Vedic Mathematics?. Sótt af http://mathlearners.com/.
- Wikipedia, the free encyclopedia. Indian mathematics. Sótt af https://en.wikipedia.org/wiki/Indian_mathematics#Vedic_period.
