 Til þess að svara því geri ég ráð fyrir að lesandinn þekki hvað tvinntala (e. complex number) er, hvernig grunnaðgerðirnar samlagning, frádráttur, margföldun og deiling eru framkvæmdar á þeim, hvað samfellt fall (e. continuous function) er og að mengi tvinntalnanna myndi sléttu (e. plane) sem er táknuð með \(C\), þannig að tvinntalan \(x + iy\) samsvari punktinum \((x,y)\). Það hjálpar einnig að þekkja pólþáttun tvinntalna \(re^{i\theta }\).
Til þess að svara því geri ég ráð fyrir að lesandinn þekki hvað tvinntala (e. complex number) er, hvernig grunnaðgerðirnar samlagning, frádráttur, margföldun og deiling eru framkvæmdar á þeim, hvað samfellt fall (e. continuous function) er og að mengi tvinntalnanna myndi sléttu (e. plane) sem er táknuð með \(C\), þannig að tvinntalan \(x + iy\) samsvari punktinum \((x,y)\). Það hjálpar einnig að þekkja pólþáttun tvinntalna \(re^{i\theta }\).
Sérhver tvinntala \(z\neq 0\) hefur tvær ferningsrætur, því að ef \(\omega ^{2}=z\) þá gildir einnig að \((-\omega) ^{2}=z\). Þetta er vandræðalegt ef við viljum tala um „ferningsrót tölunnar \(z\)“, með öðrum orðum „fallið \(\sqrt{z}\) “. Fall á að hafa eitt vel skilgreint gildi.
Þegar við skoðum ferningsrætur í mengi rauntalnanna þá er þetta vandamál auðleyst. Einungis jákvæðar rauntölur og 0 hafa rauntöluferningsrót. Við skilgreinum fallið \(\sqrt{x}\) þegar \(x\) er jákvæð sem jákvæða ferningsrót tölunnar \(x\). Fyrir tvinntölu \(z\) er aftur á móti engin eðlileg leið til að velja á kerfisbundin hátt aðra hvora ferningsrótina til að skilgreina \(\sqrt{z}\).
 Vandinn skýrist betur með eftirfarandi athugun. Skoðum hring \(H\) sem fer einu sinni kringum miðpunktinn 0 í tvinntölusléttunni, og sem byrjar og endar í punktinum z = 1. Úthlutum tölunni 1 ferningsrótina 1 og förum síðan af stað rangsælis og úthlutum hverri tölu á hringnum ferningsrót þannig að sú ferningsrót verði samfellt fall á hringnum. Það er aðeins ein leið til að framkvæma þetta, að minnsta kosti til að byrja með, og það er að úthluta tölunni \(e^{i\theta }\) ferningsrótinni \(e^{i\theta/2 }\) þar sem \(\theta\) er á bilinu frá 0 að \(2\pi\). Þegar við komum að \(i\) er ferningsrótin \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\). Þegar við komum að -1 er ferningsrótin \(i\). Þegar komið er að \(-i\) er ferningsrótin \(-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\). Nú komum við aftur að 1 en ferningsrótin er orðin -1. Þetta sýnir að það sé ómögulegt að úthluta hverri tvinntölu \(z\) ferningsrót þannig að úr verði fall sem er samfellt alls staðar í tvinntölusléttunni.
Vandinn skýrist betur með eftirfarandi athugun. Skoðum hring \(H\) sem fer einu sinni kringum miðpunktinn 0 í tvinntölusléttunni, og sem byrjar og endar í punktinum z = 1. Úthlutum tölunni 1 ferningsrótina 1 og förum síðan af stað rangsælis og úthlutum hverri tölu á hringnum ferningsrót þannig að sú ferningsrót verði samfellt fall á hringnum. Það er aðeins ein leið til að framkvæma þetta, að minnsta kosti til að byrja með, og það er að úthluta tölunni \(e^{i\theta }\) ferningsrótinni \(e^{i\theta/2 }\) þar sem \(\theta\) er á bilinu frá 0 að \(2\pi\). Þegar við komum að \(i\) er ferningsrótin \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\). Þegar við komum að -1 er ferningsrótin \(i\). Þegar komið er að \(-i\) er ferningsrótin \(-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\). Nú komum við aftur að 1 en ferningsrótin er orðin -1. Þetta sýnir að það sé ómögulegt að úthluta hverri tvinntölu \(z\) ferningsrót þannig að úr verði fall sem er samfellt alls staðar í tvinntölusléttunni.
Við þessu eru tvö svör. Við getum sett upp girðingu þannig að bannað yrði að fara umhverfis 0 og koma aftur í sama stað og byrjað var. Þetta er oft gert með því að tala um að „skera“ sléttuna frá 0 eftir geisla og er þessi skurður þá yfirleitt gerður eftir neikvæða rauntöluásnum. Í skornu sléttunni skilgreinum við ferningsrótina \(\sqrt{z}=\sqrt{r}e^{i\theta/2}\), þar sem \(z=re^{i\theta }\), \(r\geq 0\) og \(-\pi < \theta < \pi\). Við útilokum neikvæða rauntöluásinn með því að banna að \(\theta\) sé \(\pm \pi\). Þetta fall er vel skilgreint og samfellt (reyndar fágað, e. analytic function) í skornu sléttunni. Það kallast aðalferningsrótin.
Önnur lausn á þessum vanda leiðir til Riemann-flata. Við segjum þá að punkturinn 1 sem við komum að þegar við höfum farið einu sinni umhverfis 0 sé ekki sá sami og punkturinn 1 sem við byrjuðum á. Þetta eru tveir ólíkir punktar, sem báðir líta þó út eins og 1 en hafa ólíkar ferningsrætur, +1 og -1. Höldum nú ferðinni áfram og tökum annan hring umhverfis 0 og úthlutum um leið ferningsrót með samfelldum hætti. Að lokinni seinni umferðinni komum við aftur að punktinum 1 en ferningsrótin er komin aftur að 1. Það þýðir að eftir tvo hringi lendum við á sama punkti 1 og við byrjuðum á.
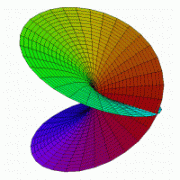 Riemann ímyndaði sér eftirfarandi uppbyggingu. Tökum tvö eintök af tvinntölusléttunni sem liggja á sama stað. Þannig liggur \(i\) á fleti nr. 1 á sama stað og \(i\) á fleti nr. 2 og svo framvegis. Nú skerum við báðar sléttur eftir neikvæðu rauntöluásunum. Síðan tengjum við efri brún skurðarins á sléttu nr. 1 við neðri brún skurðarins á sléttu nr. 2 og efri brún skurðar á sléttu nr. 2 við neðri brún sléttu nr. 1. (Efri brún þýðir hér brúnin þar sem þverhlutinn (e. imaginary part) er jákvæður, neðri brún þar sem þverhlutinn er neikvæður.) Útkoman er samanhangandi flötur þar sem hægt er að skilgreina ferningsrót sem samfellt fall (reyndar fágað fall). En lesandinn mun fljótlega sjá, ef hann reynir að búa flötinn til með pappír, skæri og límbandi, að ekki er hægt að framkvæma þessar tengingar í þrívíðu rúmi.
Riemann ímyndaði sér eftirfarandi uppbyggingu. Tökum tvö eintök af tvinntölusléttunni sem liggja á sama stað. Þannig liggur \(i\) á fleti nr. 1 á sama stað og \(i\) á fleti nr. 2 og svo framvegis. Nú skerum við báðar sléttur eftir neikvæðu rauntöluásunum. Síðan tengjum við efri brún skurðarins á sléttu nr. 1 við neðri brún skurðarins á sléttu nr. 2 og efri brún skurðar á sléttu nr. 2 við neðri brún sléttu nr. 1. (Efri brún þýðir hér brúnin þar sem þverhlutinn (e. imaginary part) er jákvæður, neðri brún þar sem þverhlutinn er neikvæður.) Útkoman er samanhangandi flötur þar sem hægt er að skilgreina ferningsrót sem samfellt fall (reyndar fágað fall). En lesandinn mun fljótlega sjá, ef hann reynir að búa flötinn til með pappír, skæri og límbandi, að ekki er hægt að framkvæma þessar tengingar í þrívíðu rúmi.
Samt er hér vel skilgreindur flötur og ekki torskilinn heldur. Ferningsrótin er gagntækt (e. bijective) fall á honum og er myndmengi þess venjulega tvinntölusléttan \(C\). Þessi Riemann-flötur er grannfræðilega séð eins og \(C\).
Hugmyndin sem hér var lýst hefur víðtækt alhæfingargildi. Athugið að ferningsrót er fall \(\omega\) sem uppfyllir \(\omega ^{2}=z\). Látum \(P(z,\omega)\) vera margliðu í tveimur breytum, til dæmis \(P(z,\omega)=\omega ^{2}-z^{3}-z-1\). Svipaða aðferð má þá nota til að búa til Riemann-flöt þar sem lausn \(\omega =\omega (z)\) á jöfnunni \(P\left ( z,\omega \right )=0\) má skilja sem vel skilgreint fall. Slíkt fall kallast algebrulegt fall. Í tilfelli ferningsrótarinnar var \(P\left ( z,\omega \right )=\omega ^{2}-z\). Þessir fletir kunna að vera flóknari frá sjónarhóli fræðigreinarinnar grannfræði (e. topology). Almennt eru þeir sléttur með endanlega mörgum handföngum. Til er einföld formúla til að reikna út fjölda handfanga út frá margliðunni \(P(z,\omega)\). Þessi fjöldi kallast kyn flatarins. Riemann-fletir voru þess vegna upphaf grannfræði.
Það að ekki er hægt að byggja fletina í þrívíðu rúmi samkvæmt lýsingunni sem við gáfum gæti talist ókostur. Stærðfræðingar líta því stundum öðrum augum á Riemann-fleti til að skilja þá. Eitt sjónarmið er til dæmis að skilja Riemann-flötinn fyrir algebrulega fallið \(\omega =\omega (z)\), sem leysir \(P\left ( z,\omega \right )=0\), sem ekkert annað en mengi allra tvennda \((z,w)\) sem fullnægja jöfnunni \(P(z,w)=0\). Þetta mengi er engan veginn torskilið, það er hlutmengi í margfeldinu \(C\times C\) og hefur í flestum tilfellum þægilega grannfræðilega eiginleika því það er flötur (surface). Fallið \(\omega(z)\) má nú túlka sem ofanvarpið \((z,\omega) \mapsto \omega\) einskorðað við þennan flöt.
Þeir stærðfræðingar sem líta fremur á sig sem algebrufræðinga en grannfræðinga hafa þá venju að kalla fletina, sem við lýstum hér á undan, ferla og getur þetta valdið misskilningi. Ástæðan fyrir venjunni er þessi: Ef \(x\) og \(y\) eru rauntölur þá skilgreinir jafna af gerðinni \(P(x,y)=0\) feril, en frá algebrulegu sjónarmiði er stundum þægilegt að líta á lausnarmengi \(P(z,\omega )=0\), þegar um tvinntölur eru að ræða, sem feril jafnvel þótt það sé flötur frá grannfræðilega sjónarmiði. Til dæmis er tvinntalnasléttan stundum kölluð lína af sömu ástæðu.
Af þessum „ferlum“ eru sporgeru ferlarnir (e. elliptic curves) frægastir. Þeir eru Riemann-fletir af kyni 1, til dæmis eins og þeir sem koma fram í sambandi við jöfnur af gerðinni \(\omega ^{2}=z^{3}+az+b\). Þessir fletir eru frekar einfaldir grannfræðilega séð, enda eru þeir allir hjólfletir (torus; nánar tiltekið vantar einn punkt sem svarar til óendanlegs). Krefjandi verkefni er að finna ræða punkta á þessum flötum. Þetta tengist verkefni um díófantískar jöfnur og er frægast þeirra verkefni Fermats: Að finna heiltölur \(a\), \(b\), \(c\) þannig að \(a^{n}+b^{n}=c^{n}\). Þetta sést á þeirri staðreynd að ræð lausn á \(\omega ^{n}+z^{n}=1\) gefur heiltölulausn á \(a^{n}+b^{n}=c^{n}\). Það voru djúp tengsl þessa verkefnis við talnafræðilega eiginleika sporgerra ferla sem leiddu til lausnar á síðustu setningu Fermats. Frekara lesefni og myndir
- Hefur tilgáta Riemanns verið sönnuð? eftir Ragnar Sigurðsson.
- Mynd af Riemann er af Bernhard Riemann. Wikipedia, frjálsa alfræðiorðabókin.
- Mynd a hring er af Visualizing Complex Functions. Xaq's Homepage.
- Mynd af Riemann-fleti er af Summer Tutorials 2003. Harvard Mathematics Department.
