Hvers vegna léttist átak við að "dobla" það með blökkum? Er hægt að "dobla" átak endalaust þannig að hægt sé að lyfta 100 tonnum með annarri hendi, svo dæmi sé tekið?Áhaldið sem við köllum blökk, trissu eða skoruhjól (e. pulley) er gamalt. Líta má á það sem eins konar vogarstöng (lever). Við notum trissur einkum á tvo vegu, í fyrsta lagi þannig að ás hennar sé fastur en í öðru lagi þannig að hún leikur laus í ramma á bandinu og færist þegar togað er í það. Í fyrra tilvikinu verkar trissan eins og vogarstöng sem er til dæmis hengd upp í miðpunkti, við togum í hægri endann niður á við og vinstri endinn færist upp á við. Báðir endarnir færast jafnlangt og stærð kraftsins breytist ekki; vogarstöngin verkar í þessu tilviki með jafnmiklum krafti upp á við vinstra megin eins og við beitum niður á við hægra megin. Þegar ásinn í trissu er hengdur eða festur upp (sjá mynd að neðan, til vinstri) hegðar trissan sér nákvæmlega eins: Lyftikrafturinn hægra megin er jafnstór og togkrafturinn sem við beitum á bandið vinstra megin. Við lyftum hlutnum hægra megin jafnlangt og við togum bandið vinstra megin. Það eina sem breytist í báðum þessum dæmum er stefna kraftsins því að krafturinn frá okkur vísar niður á við en krafturinn á hlutinn sem við erum að lyfta vísar upp. Þetta getur vissulega skipt máli í ýmsum dæmum.
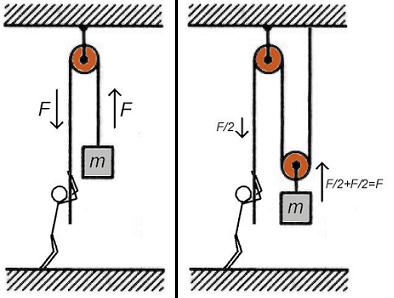
En við getum líka notað vogarstangir eins og járnkarla, hrífusköft eða sköft á matskeiðum til að breyta krafti og færslu. Ef hægri endinn á vogarstönginni er fastur, við hengjum hlut í miðpunkt hennar og lyftum vinstri endanum, þá þurfum við aðeins að beita krafti sem nemur helmingi af þyngd hlutarins. Þetta gerist þó ekki "ókeypis" því að við þurfum að færa vinstri endann tvöfalt lengri leið en hluturinn fer. Ef við festum nú upp endann á bandi og leggjum bandið um trissu með lóði í, þá gerist nákvæmlega það sama þegar við togum í bandið upp á við: Við þurfum aðeins að beita hálfum krafti til að lyfta lóðinu en þurfum hins vegar að draga bandið tvöfalt lengri vegalengd en lóðið fer. Ef okkur finnst óþægilegt að toga upp á við getum við til dæmis lagt bandið yfir trissu sem er föst við loftið og togað síðan niður á við (sjá mynd að ofan, til hægri). Ef við ráðum ekki við að lyfta lóðinu með þessum búnaði getum við tekið enn eina trissu og fest við þá fyrstu þannig að þær hreyfist saman. Með því helmingum við kraftinn aftur. Til að lyfta lóði sem er 200 kg þyrftum við þannig aðeins kraft sem svarar 50 kg en mundum toga bandið fjórum sinnum lengra en lóðið færist. Og svona getum við haldið áfram nokkrum sinnum eins og spyrjandi ýjar að. Þetta er þó varla hagkvæmt ef trissurnar verða mjög margar. Eigin þyngd þeirra og bandsins fer þá að segja til sín og sömuleiðis núningur, meðal annars vegna stífni í bandinu.
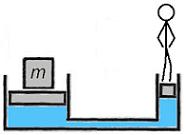 Ef spyrjandi vill lyfta mörgum tonnum "með annarri hendi" er sennilega snjallast að nota vökvalyftu eða "tjakk". Í slíku tæki hreyfum við dælu eða bullu með litlu þverskurðarflatarmáli og þrýstum þannig vökva undir stóra bullu eða flöt sem færist þá upp á við (sjá mynd). Kraftahlutfallið er þá jafnt hlutfallinu milli flatarmálanna. Við getum til dæmis hugsað okkur að minni bullan sé 5 fersentímetrar í þverskurð en sú stærri 5 fermetrar. Flatarmálshlutfallið er þá 100*100 = 10.000 og kraftur sem samsvarar 10 kg mundi duga til að lyfta 100 tonnunum sem spyrjandi ber fyrir brjósti.
Vogarstangir eru skemmtileg, einföld áhöld eða fyrirbæri sem blasa við allt í kringum okkur, hvert sem litið er. Margir, þar á meðal lærðir kennslubókahöfundar í eðlisfræði, virðast halda að vogarstangir séu fyrst og fremst til þess að margfalda kraftinn. Svo er hins vegar alls ekki því að hitt er alveg eins algengt að þær margfaldi færsluna og minnki þá kraftinn sem því svarar eins og áður var lýst.
Hrífur eru dæmi um þetta því að með þeim margföldum við hreyfingu handanna en minnkum kraftinn. Fingurnir á mér eru annað dæmi um þetta þar sem ég sit og "slæ" þennan texta inn á hnappaborð tölvunnar. Þeir magna upp litlar hreyfingar í vöðvunum í höndunum. Og þegar ég hreyfi handlegginn magnast upp lítil hreyfing sem upphandleggsvöðvinn veldur í olnboganum. Fróðlegt dæmi um vogarstangir, kraft og færslu fæst með því að hugleiða skæri af ýmsum gerðum. Við vitum til dæmis að klæðskurðarskæri eru allt öðru vísi en naglaskæri og það er ekki að ástæðulausu. Dúkhnífur er líka býsna ólíkur pappírshníf í lögun, af svipuðum ástæðum.
Mannkynið hefur í árþúsundir notað áhöld eins og vogarstangir og trissur til að létta sér lífið við ýmis verk. Fimm áhöld, vogarstöngin, fleygurinn, skrúfan, trissan og hjól með öxli eru stundum sameiginlega kölluð einfaldar vélar (simple machines).
Áhaldið hjól á öxli er í rauninni náskylt vogarstönginni og er oft notað þannig að fleiri en eitt hjól sitja á sama öxli eða tengjast með öðrum hætti. Þetta er mikið notað kringum okkur nú á dögum því að það er að finna til dæmis í gírum á reiðhjólum og bílum og í hvers konar sveifarhjólum og tannhjólakerfum. Í þessum mikilvægu hlutum í tækni nútímans eru menn sem sagt enn að nota svipaðar hugmyndir og tækni og beitt var þegar pýramídarnir í Egyptalandi voru byggðir fyrir næstum fimm þúsund árum.
Sjá einnig svör um lögmál Newtons eftir sama höfund.
Ef spyrjandi vill lyfta mörgum tonnum "með annarri hendi" er sennilega snjallast að nota vökvalyftu eða "tjakk". Í slíku tæki hreyfum við dælu eða bullu með litlu þverskurðarflatarmáli og þrýstum þannig vökva undir stóra bullu eða flöt sem færist þá upp á við (sjá mynd). Kraftahlutfallið er þá jafnt hlutfallinu milli flatarmálanna. Við getum til dæmis hugsað okkur að minni bullan sé 5 fersentímetrar í þverskurð en sú stærri 5 fermetrar. Flatarmálshlutfallið er þá 100*100 = 10.000 og kraftur sem samsvarar 10 kg mundi duga til að lyfta 100 tonnunum sem spyrjandi ber fyrir brjósti.
Vogarstangir eru skemmtileg, einföld áhöld eða fyrirbæri sem blasa við allt í kringum okkur, hvert sem litið er. Margir, þar á meðal lærðir kennslubókahöfundar í eðlisfræði, virðast halda að vogarstangir séu fyrst og fremst til þess að margfalda kraftinn. Svo er hins vegar alls ekki því að hitt er alveg eins algengt að þær margfaldi færsluna og minnki þá kraftinn sem því svarar eins og áður var lýst.
Hrífur eru dæmi um þetta því að með þeim margföldum við hreyfingu handanna en minnkum kraftinn. Fingurnir á mér eru annað dæmi um þetta þar sem ég sit og "slæ" þennan texta inn á hnappaborð tölvunnar. Þeir magna upp litlar hreyfingar í vöðvunum í höndunum. Og þegar ég hreyfi handlegginn magnast upp lítil hreyfing sem upphandleggsvöðvinn veldur í olnboganum. Fróðlegt dæmi um vogarstangir, kraft og færslu fæst með því að hugleiða skæri af ýmsum gerðum. Við vitum til dæmis að klæðskurðarskæri eru allt öðru vísi en naglaskæri og það er ekki að ástæðulausu. Dúkhnífur er líka býsna ólíkur pappírshníf í lögun, af svipuðum ástæðum.
Mannkynið hefur í árþúsundir notað áhöld eins og vogarstangir og trissur til að létta sér lífið við ýmis verk. Fimm áhöld, vogarstöngin, fleygurinn, skrúfan, trissan og hjól með öxli eru stundum sameiginlega kölluð einfaldar vélar (simple machines).
Áhaldið hjól á öxli er í rauninni náskylt vogarstönginni og er oft notað þannig að fleiri en eitt hjól sitja á sama öxli eða tengjast með öðrum hætti. Þetta er mikið notað kringum okkur nú á dögum því að það er að finna til dæmis í gírum á reiðhjólum og bílum og í hvers konar sveifarhjólum og tannhjólakerfum. Í þessum mikilvægu hlutum í tækni nútímans eru menn sem sagt enn að nota svipaðar hugmyndir og tækni og beitt var þegar pýramídarnir í Egyptalandi voru byggðir fyrir næstum fimm þúsund árum.
Sjá einnig svör um lögmál Newtons eftir sama höfund.
