1, 2, 3, ...Að vísu getum við ekki skrifað þessa runu niður, vegna þess að við getum ekki skrifað niður nema endanlega mörg tákn, en það breytir því ekki að runan er til. Annað dæmi um endalausa runu er þessi runa:
1/1, 1/2, 1/4 ...Hér höfum við runu ræðra talna þar sem hver tala, að þeirri fyrstu undanskilinni, er helmingi lægri en talan á undan. En þótt þessi dæmi séu einföld og hafi yfirbragð þess sem er augljóst, þá getur gamanið kárnað. Í fornöld setti Zenon (um 470 fyrir Krist) fram nokkrar þverstæður sem áttu að sýna að hreyfing gæti ekki átt sér stað. Ein þverstæðan er eitthvað á þessa leið: Við byrjum á að tilgreina tvo staði, A og B, á beinni línu eins og hér að neðan.
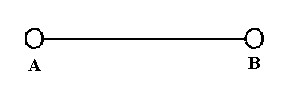
Vegalengdina frá A til B köllum við [AB]. Hugsum okkur nú að maður nokkur vilji fara frá A til B. Áður en hann kemst til B þarf hann augljóslega fyrst að komast helming leiðarinnar, með öðrum orðum, hann þarf fyrst að fara frá A vegalengdina [AB]/2.
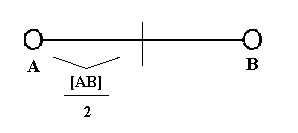
Zenon benti svo á að maðurinn þyrfti að helminga afgang leiðarinnar, og svo að helminga þann helming og þannig út í hið óendanlega, og því kæmist hann aldrei á leiðarenda. Við getum snúið þessari röksemdafærslu við og litið á það sem þarf að gerast áður en maðurinn kemst helming leiðarinnar. Áður en maðurinn kemst svo langt sem [AB]/2, þarf hann að fara helming þeirrar leiðar. Með öðrum orðum þarf hann að fara vegalengd sem er fjórðungur af leiðinni frá A til B, [AB]/4, áður en hann klárar helming leiðarinnar. Og svona gengur það koll af kolli án nokkurs enda. Eftirfarandi runa lýsir þessu helmingunarferli:
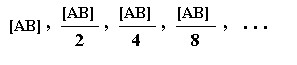
Þessi runa er endalaus og ætli maður að hugsa til enda, áður en maður leggur af stað, hvernig maður kemst frá A til B með því að helminga alltaf hvern áfanga á leiðinni, þá kemst maður aldrei af stað. Að minnsta kosti ekki ef það að hugsa ferli til enda krefst þess að hverju skrefi sé veitt einhver athygli. Reyndar er ekki auðvelt að segja hvað það er að hugsa eitthvað til enda, og ekki ljóst að til þess að hugsa tiltekið ferli til enda þurfi að huga að hverju skrefi. Hugsum okkur bílstjóra sem þarf að fara á tiltekinn stað. Hann getur lagt nákvæmlega niður fyrir sig hvaða götur hann ætlar að fara áður en hann leggur af stað, og þar með getum við kannski sagt að hann hugsi til enda hvernig hann ætlar að komast á leiðarenda áður en hann leggur af stað. En þó þarf ekki að vera að bílstjórinn hafi leitt hugann að því hvenær hann ætli að stíga á bremsuna, hversu hratt hann ætli að keyra, né hvað hann ætli að gera fari eitthvað úrskeiðis. Að keyra bíl frá einum stað til annars er ferli sem er takmarkað, bæði í tíma og rúmi. Og þó er ekki ljóst hvað það þýðir að hugsa það til enda. En látum þennan vanda liggja milli hluta í bili. Við skulum gefa okkur einhvern hversdagslegan skilning á hugmyndinni um að hugsa eitthvað til enda og spurja svo hvort það sé á einhvern hátt í grundvallaratriðum erfiðara að hugsa til enda það sem er óendanlegt heldur en það sem er endanlegt. Þýski stærðfræðingurinn David Hilbert sagði eitt sinn frá hóteli sem hafði óendanlega mörg herbergi. Hilbert sagði þessa sögu til að skýra hvernig á því mætti standa að summa tveggja óendanlega stórra talna gæti verið jafn há hvorri tölu um sig. Samlagning óendanlega stórra talna er ekki okkar vandamál, en við getum notað sögu Hilberts til að varpa ljósi á það hvort hægt sé að hugsa til enda eitthvað sem er óendanlegt. Á hótelinu eru óendanlega mörg herbergi, en samt er það fullbókað. Það er gestur í hverju herbergi. En ekki er nóg með að það sé gestur í hverju herbergi heldur ber að garði rútu með óendanlega mörgum gestum sem allir vilja fá að gista á hótelinu. Til að ráða fram úr þessum vanda kann hótelstjórinn eitt ráð. Hann biður gestinn í herbergi 1 að færa sig um eitt herbergi, gestinn í herbergi tvö að færa sig um tvö herbergi, gestinn í herbergi þrjú að færa sig um þrjú herbergi og svo framvegis. Úr því að það eru óendanlega mörg herbergi á hótelinu þarf hótelstjórinn ekki að hafa neinar áhyggjur af því að tilfærslurnar sigli í strand. Og nú má spyrja hvort eitthvað sé því til fyrirstöðu að hótelstjórinn hafi hugsað þessar tilfærslur til enda. Öll herbergin eru númeruð og hótelstjórinn hugsar sér einfaldlega að gesturinn í herbergi n, þar sem n er einhver náttúruleg tala, færi sig um n herbergi. En ef hótelstjórinn hefur hugsað tilfærslurnar til enda þá hefur hann líka hugsað til enda eitthvað sem er endalaust þar sem herbergin eru, eins og áður segir, óendanlega mörg. Dæmið af hótelinu óendanlega virðist því renna stoðum undir að hægt sé að hugsa til enda jafnvel það sem er óendanlegt. En sá galli er á dæminu að það er ekki raunverulegt. Hótel eru ekki svona stór nema kannski í ævintýrunum og það sem er hægt að gera í ævintýrum gengur ekki alltaf upp í veruleikanum. En vendum þá kvæði okkar í kross og hugum að talsvert ólíku dæmi. Heimspekingar hafa lengi velt fyrir sér eðli sannleikans og því hvernig mætti skilgreina umsögnina sannur/sönn. Árið 1935 setti pólski stærðfræðingurinn og heimspekingurinn Alfred Tarski fram skilgreiningu á umsögninni sönn fyrir setningar í tilteknum formlegum málum eins og máli stærðfræðinnar. Tarski sagði að slík skilgreining þyrfti að uppfylla tvö skilyrði. Annars vegar mætti hún ekki leiða til mótsagnar og hins vegar þyrfti að vera hægt að leiða út það sem við getum kallað T-jafngildi fyrir hverja setningu í tungumálinu. Tarski notaði gjarnan setninguna „Snjór er hvítur” sem dæmi en fyrir þá setningu þarf að vera hægt að leiða út jafngildið:
Setningin „snjór er hvítur” er sönn ef og aðeins ef snjór er hvítur.Nú getum við hugsað okkur að nota stafinn „S” sem breytu fyrir hvaða setningu sem er en þá getum við skrifað niður T-jafngildi fyrir allar setningar tungumálsins í einni línu.
Setningin „S” er sönn ef og aðeins ef S.Og þar sem alltaf má búa til nýjar setningar er T-jafngildið í raun fullyrðing um óendanlega margar setningar. Menn eru ekki sammála um hvort Tarski hafi hugsað skilgreiningu sína á sannleikshugtakinu til enda en flestir eru þeirrar skoðunar að hvaða meinbugir sem kunni að vera á kenningu Tarskis þá sé meinið ekki að setningarnar sem hún fjallar um séu óendanlega margar. Við getum því leyft okkur að segja að það sé vel hægt að hugsa til enda það sem er endalaust, að minnsta kosti þangað til við fáum betri skilning á því hvað það er að hugsa eitthvað til enda. Heimild: Alfred Tarski, „Merkingarfræðilega hugmyndin um sannleikann og undirstöður merkingarfræðinnar”, í Heimspeki á tuttugustu öld, Mál og menning 1994.
