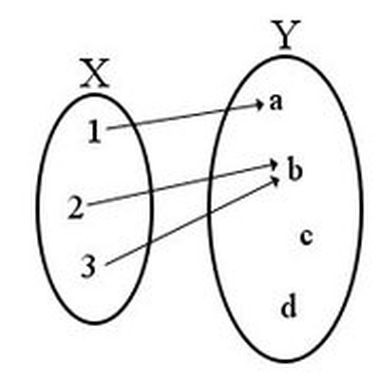
2, 4, 6, 8, 10, 12, 14, ... ogbáðar runur; sú fyrri er gefin með fallinu f(n) = 2n, en í þeirri seinni eru aukastafir pí taldir upp. Allar runur sem við munum skoða hafa óendanlega marga meðlimi. Það takmarkar okkur ekki, því ef við rekumst á einhverja runu sem tekur enda, þá getum við breytt henni í óendanlega runu með því að endurtaka síðustu töluna í henni að eilífu. Þegar stærðfræðingar tala um óendanlegan fjölda gera þeir greinarmun á teljanlegum- og óteljanlegum óendanleika. Ef við eigum teljanlega marga hluti, þá þýðir það að við getum parað þá einn af öðrum með tölunum 1, 2, 3, ..., og fjöldi þeirra er endanlegur eða jafn fjölda náttúrlegu talnanna. Við getum hins vegar verið með það marga hluti að þeir eru fleiri en náttúrlegu tölurnar, og þá segjum við að fjöldi þeirra sé óteljanlegur. Sem dæmi eru sléttu tölurnar teljanlega margar, en rauntölurnar eru óteljanlega margar. Nú liggur auðvitað beint við að spyrja sig hvort til séu teljanlega eða óteljanlega margar runur?
1, 4, 1, 5, 9, 2, 6, ...
Fljótséð er að það eru til óteljanlega margar mismunandi runur: Við fáum eina runu fyrir hverja náttúrlega tölu n með því að fara gegnum margföldunartöfluna fyrir n, eins og við gerðum hér að ofan þegar við settum n jafnt 2 og fengum sléttu tölurnar. Ef við hugsum okkur um í smástund sjáum við þó að það eru að minnsta kosti til jafn margar runur og rauntölur, því ef við höfum einhverja rauntölu getum við búið til rununa sem telur upp tölustafina í tugabrotaframsetningu rauntölunnar. Þar sem það eru til óteljanlega margar rauntölur, þá eru líka til óteljanlega margar runur. En þá skulum við snúa okkur að reglunum. Við skulum segja að það sé til regla sem býr til runu ef það er hægt að láta tölvu gefa okkur tölurnar í rununni, því það samsvarar ágætlega þeim hugmyndum sem við höfum um reglur. Þá eru til reglur fyrir báðar runurnar okkar að ofan, því sú fyrri er einfaldlega gefin með formúlu, og ef við höfum nægan tíma þá er hægt að láta tölvu reikna eins marga aukastafi í pí og við viljum, og gefa þá einn af öðrum. Þar sem það eru til margar mismunandi tölvur í dag, þá væri best að við kæmum okkur saman um hvernig tölvu við ætlum að nota. Í tölvunarfræði er oft notast við svokallaðar Turing-vélar þegar á að líkja eftir nútímatölvum, og þær henta ágætlega hér. Á meðan fræðilega skilgreiningin á Turing-vél er háð ýmsum smáatriðum, þá er einfalt að lýsa þeim með beinum orðum: Turing-vél er kassi sem flakkar fram og til baka á óendanlega löngum minnisborða, og getur bæði lesið tákn af honum, skrifað á hann, og breytt þeim táknum sem eru á borðanum.

Sérhver Turing-vél er aðeins hönnuð til að vinna eitt verk. Þannig er til Turing-vél sem gerir ekkert annað en að leggja saman tvo og þrjá, önnur Turing-vél sem getur aðeins margfaldað gefna tölu með fimm, og aðrar sem vinna einhver flóknari verk. Við fyrstu sýn virðast þetta mjög einfaldar og takmarkaðar vélar, og því kemur flestum verulega á óvart að allt sem er hægt að gera með tölvum í dag má gera með Turing-vélum. Fyrir okkur þýðir þetta að við getum sagt að á bakvið gefna runu sé regla ef það er til Turing-vél sem gefur okkur tölurnar í rununni. Þetta reynist vera lykilatriðið sem þarf til að svara upphaflegu spurningunni, því þegar maður skoðar formlegu skilgreininguna á Turing-vél kemur í ljós að það eru bara til teljanlega margar slíkar vélar. Við munum að það eru til óteljanlega margar runur, svo þar af leiðir að það eru til runur sem engin regla er á bakvið. Vegna þess að slíkar runur eru í eðli sínu mjög flókin fyrirbæri treystum við okkur þó ekki til að benda á dæmi um þannig runu hér. Þeir sem hafa áhuga á runum af þessu tagi ættu að kynna sér reiknanleika og reiknanleg föll í fræðilegri tölvunarfræði. Frekara lesefni af Vísindavefnum:
- Hvort eru fleiri mínus- eða plústölur í talnakerfi okkar? eftir Stefán Inga Valdimarsson og Ögmund Jónsson.
- Hvað felst í vandamálinu ,,P vs. NP''? eftir Erlend S. Þorsteinsson.
- Hefur talnarunan 4, 8, 15, 16, 23, 42 sem kemur fyrir í Lost, einhverja stærðfræðilega merkingu? eftir Gunnar Þór Magnússon.
- Carothers, N.L. Real analysis. Cambridge University Press, 1999.
- Sipser, Michael. Introduction to the Theory of Computation. PWS Publishing, 1997.
- Grein um reiknanleika af Wikipedia.
- Allar myndir fengnar af Wikipedia.