Sólin
Rís 11:20 • sest 15:29
Tunglið
Rís 18:59 • Sest 14:11
Flóð
Árdegis: 08:15 • Síðdegis: 20:42
Fjara
Árdegis: 01:58 • Síðdegis: 14:37
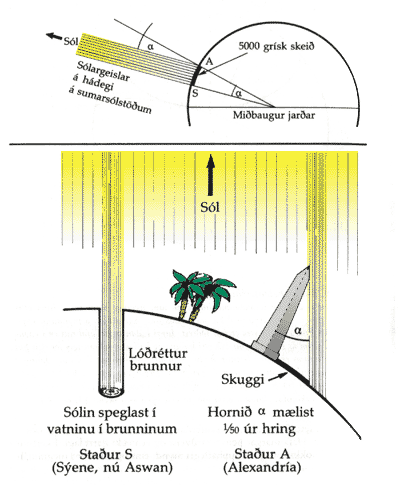
Eratosþenes vissi að á hádegi um hásumar falla ljósgeislar frá sólinni beint ofan í brunn í borginni Sýenu við Níl. Sólin er því beint yfir henni á þessum tíma. Með því að mæla hversu löngum skugga sólin varpar einhvers staðar annars staðar á sama tíma og vita fjarlægðina milli þessara tveggja staða gat hann reiknað ummál jarðar. Hér eru þó ýmis ljón í veginum. Í fyrsta lagi voru engar nákvæmar klukkur til á tímum Eratosþenesar. Því gat hann ekki stillt klukku í Sýenu og farið með hana annað. Þetta er þó nauðsynlegt því að hann þarf að mæla lengd skuggans þegar sólin er í hádegisstað í Sýenu. Eratosþenes komst framhjá þessu vandamáli með því að geta sér þess til að borgin Alexandría væri á sama lengdarbaug og Sýena. Þá er sólin í hádegisstað í þessum tveimur borgum á sama tíma. Þessi nálgun stenst ágætlega. Næsta vandamál var að meta fjarlægðina milli Sýenu og Alexandríu. Án allrar mælitækni er besta aðferðin til að meta fjarlægðir sú að ganga þær og líklega voru þær fjarlægðarmælingar sem Eratosþenes notaði gerðar með þeirri aðferð. Í öllu falli mat hann fjarlægðina milli Sýenu og Alexandríu vera 5.000 grísk skeið, en sú lengdareining var miðuð við íþróttavelli Forn-Grikkja. Loks mældi hann hornið milli sólarljóss og lóðréttrar stangar í Alexandríu með því að mæla hlutfallið milli hæðar og lengdar skugga sem sólin varpaði í hádegisstað um hásumar. Hann komst að þeirri niðurstöðu að hornið svaraði til eins fimmtugasta af heilum hring. Þannig fékk hann út að fjarlægðin milli Sýenu og Alexandríu væri einn fimmtugasti af ummáli jarðar, það er að ummál jarðar væri 50 * 5.000 skeið = 250.000 skeið. Þegar meta á gæði þessarar mælingar Eratosþenesar þurfum við að vita lengd skeiðsins. Það var hins vegar ekki vel stöðluð eining því að lengd íþróttavalla gat legið á bilinu 150 til 220 metrar. Líklegt er þó að skeiðið sem Eratosþenes notaði hafi verið 185 metrar og samkvæmt því hefur honum reiknast ummál jarðar vera um 46.000.000 metrar. Þessi tala er um 15% stærri en raunverulegt gildi en engu að síður verður að telja mælingu Eratosþenesar afar góða miðað við þau mælitæki sem honum stóðu til boða. Lesefni: Þorsteinn Vilhjálmsson, 1986. Heimsmynd á hverfanda hveli I. Reykjavík: Mál og menning.
