Hvernig virkar kosningakerfið á Íslandi, hvað þurfa flokkar mikla kosningu til að koma manni á þing o.s.frv.?Gagnlegt er fyrir lesandann að kynna sér fyrst svar við spurningunni Hvernig virkar kosningakerfið á Íslandi? Eins og í því svari verður hér til skýringar stuðst við úrslit kosninga til Alþingis 29. október 2016. Í upphafi er rétt að rifja upp hvernig þingsætum er úthlutað í nokkrum meginskrefum:
- Kjördæmissætum er úthlutað til lista í hverju kjördæmi.
- Fundið er hvaða flokkar koma til álita við uppskiptingu jöfnunarsæta að teknu tilliti til 5% þröskuldar.
- Jöfnunarsætunum er síðan ráðstafað til einstakra lista.
- Að lokum er að finna hvaða frambjóðendur hafa náð kosningu í þau sæti sem listi þeirra hlýtur.
Kosning í kjördæmissæti
Lítum fyrst á úthlutun kjördæmissæta í Norðvesturlandskjördæmi í kosningunum 2016 sem kemur fram í töflu 1.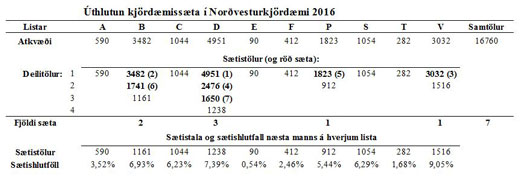
Tafla 1: Í efstu línu eru atkvæðatölur og síðan atkvæði á einstök sæti lista, sætistölur þeirra. Sætistölur lista eru atkvæðatala listans deilt með deilitölunum 1, 2, 3 og svo framvegis. Kjördæmissætin eru sjö og svara til sjö hæstu sætistalnanna sem eru feitletraðar, en stærðarröð þeirra er sýnd innan sviga.
Lágmarksfylgi sem tryggir kjördæmissæti
Almenna reglan er sú að lista er tryggt kjördæmissæti ef sætishlutfall hans er yfir vissu lágmarkshlutfalli, sem hér verður nefnt efra lágmark sætishlutfalls eða til styttingar efra lágmark. Þetta efra lágmark reiknast sem 1 á móti tölu kjördæmissætanna að einum viðbættum. Víkjum aftur að dæminu um Norðvesturkjördæmið 2016. Þar sem kjördæmissætin eru 7 að tölu er þetta efra lágmark brotið $\frac{1}{7+1}$ eða 1/8 eða sem nemur 12,5% og svaraði í kosningunum 2016 til 2.095 atkvæða þar sem gildu atkvæði voru 16.760. Allir listar í Norðvesturkjördæmi sem höfðu sætishlutfall yfir þessu marki áttu víst sæti og það áður en landskjörstjórn hóf úthlutun sæta. Af hverju er hægt að fullyrða þetta? Fyrir þá sem hafa gaman að smá stærðfræði skulum við leiða þetta út: Segjum að heildartala kjördæmissæta sé $n$, að $m$ listar hafi verið í framboði og sá $j$-ti þeirra hafi fengið $A_j$ atkvæði. Gildu atkvæðin eru þá alls $$A:=\sum_{j=1}^m{A_j} \qquad (1)$$ Hér höfum við auðkennt formúluna sem þá fyrstu (1). Segjum nú að það sé búið að úthluta sætunum $n$ að einu undanskildu en þar af hafi $j$-ti listinn fengið $n_j$ sæti. Þar með er $$\sum_{j=1}^m{n_j}=n-1 \qquad (2)$$ Eftir situr spurningin hvaða listi eigi að hljóta $n$-ta sætið. Gefum okkur að listi númer 1 hafi fengið það mörg atkvæði að sætistala næsta sætis hans, sætis númer $n_1+1$, nái þeim lágmarksmörkum sem eiga að tryggja sæti, það er að segja efra lágmarkinu ofangreinda, eða $\frac{A_1}{n_1+1} > \frac{A}{n+1}$ en ójöfnuna má umskrifa sem $$A_1 > \frac{n_1+1}{n+1} A \qquad (3)$$ Getur verið að einhver annar listi eigi að minnsta kosti jafnmikið tilkall til þessa lokasætis, til dæmis listi númer 2? Þá væri $\frac{A_2}{n_2+1} \geq \frac{A_1}{n_1+1}$ sem má líka rita þannig $$A_2\geq\frac{n_2+1}{n_1+1} A_1 \qquad (4)$$ Með hliðsjón af ójöfnu (3) má gera úr (4) ójöfnuna $$A_2>\frac{n_2+1}{n+1} A \qquad (5)$$ En svo vitum við að öll þegar fengin sæti listanna voru með réttu á undan þessu tilvonandi sæti lista númer 1, sæti hans nr. $n_1+1$. Þar með vitum við að $\frac{A_j}{n_j}\geq\frac{A_1}{n_1+1}$ fyrir sérhvern lista $j$ þó við þurfum aðeins að nýta okkur þetta um lista númer $j=3,\dots,m$. (Vera má að $m=2$ en þá er vitaskuld þetta safn lista tómt.) Sem fyrr getum við gert úr þessum síðustu ójöfnum tvær nýjar $$A_j\geq\frac{n_j}{n_1+1} A_1 \qquad (6)$$ og síðan $$A_j>\frac{n_j}{n_1+1} A \qquad (7)$$ Ójafna (7) gildir sem sagt fyrir $j=3,\dots,m$. Þessu næst leggjum við saman ójöfnunurnar (3), (5) og (7), það er að segja vinstri og hægri hliðar þeirra, en höfum jafnframt í huga jöfnur (1) og (2). Þá má draga eftirfarandi ályktanir: $$\qquad A=\sum_{j=1}^m{A_j}=A_1 + A_2 + \sum_{j=3}^m{A_j} >\frac{n_1+1}{n+1} A + \frac{n_2 + 1}{n+1} A + \sum_{j=3}^m{\frac{n_j}{n+1}} A$$ $$ = \frac{1}{n+1} A \Big( n_1+1+n_2+1+\sum_{j=3}^m{n_j}\Big) $$ $$=\frac{1}{n+1}A\Big( 2+\sum_{j=1}^m{n_j}\Big)=\frac{1+n}{n+1} A = A \qquad (7)$$ En nú er komin upp sú mótsögn að A>A sem leiðir til þess að listi $n_1$ getur ekki átt neinn keppinaut um síðasta sætið. Hann á það tryggt þar sem hann uppfyllir skilyrðið (3). Þar með getur enginn annar listi uppfyllt það skilyrði líka! Efra lágmarkið, það lágmarksfylgi sem þarf til að eiga tryggt kjördæmissæti má lesa úr eftirfarandi töflu 2:
Tafla 2: Hér má sjá efra lágmark eða það fylgi, mælt sem hlutfall af gildum atkvæðum, sem þarf að yfirstíga til að eiga tryggt kjördæmissæti allt eftir því hvað kjósa skal í mörg sæti. Dálkurinn lengst til hægri vísar til þess hvaða fylgi tryggir jöfnunarsæti á landsvísu að því tilskyldu að flokkur hafi náð 5% þröskuldinum. Þetta er skýrt síðar í þessum pistli.
Fylgi sem dugar ekki fyrir kjördæmissæti
Nú kann lesandinn að spyrja hvers vegna D-listinn í Norðvesturlandi hafi fengið kjördæmissæti í kosningunum 2016 út á 9,85% fylgi sem er undir mörkunum sem talað er um hér undan. Þau mörk, 12,5% í þessu tilviki, segja hvað þurfi til að eiga sæti tryggt. Þar með er ekki sagt að minna fylgi geti ekki verið nægilegt í einstaka tilvikum. Því er fróðlegt að íhuga neðra lágmark, það er að segja slíkt fylgismark að fylgi undir því geti aldrei leitt til þingsætis. Slík mörk eru til, en eru ekki eins einföld í framsetningu og fyrrgreind efri mörk. Neðra lágmarkið miðast ekki aðeins við stærð kjördæmanna heldur líka tölu lista. Útleiðslan á því er nokkuð flókin og verður ekki sýnd hér, en niðurstaðan er birt í töflu 3: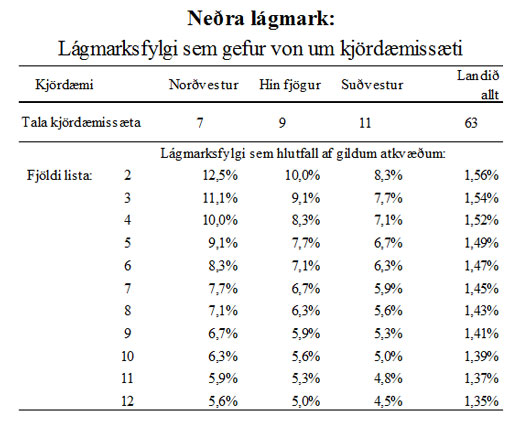
Tafla 3: Hér má sjá neðra lágmark eða það fylgi, mælt sem hlutfall af gildum atkvæðum, sem þarf til að geta átt von á kjördæmissæti allt eftir því hvað kjósa skal í mörg sæti og hve margir listar eru í framboði. Dálkurinn lengst til hægri vísar til hliðstæðs lágmarksfylgis til að ná megi jöfnunarsæti á landsvísu að því tilskyldu að flokkur hafi náð 5% þröskuldinum. Er skýrt síðar í þessum pistli.
