
Hér getur þú sent okkur nýjar spurningar um vísindaleg efni.
Hafðu spurninguna stutta og hnitmiðaða og sendu aðeins eina í einu. Einlægar og vandaðar spurningar um mikilvæg efni eru líklegastar til að kalla fram vönduð og greið svör. Ekki er víst að tími vinnist til að svara öllum spurningum.
Persónulegar upplýsingar um spyrjendur eru eingöngu notaðar í starfsemi vefsins, til dæmis til að svör verði við hæfi spyrjenda. Spurningum er ekki sinnt ef spyrjandi villir á sér heimildir eða segir ekki nægileg deili á sér.
Spurningum sem eru ekki á verksviði vefsins er eytt.
Að öðru leyti er hægt að spyrja Vísindavefinn um allt milli himins og jarðar!

4.10.2000
Guðmundur Ingi, fæddur 1982
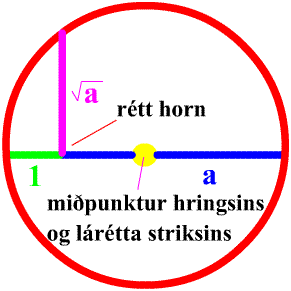
Stefán Ingi Valdimarsson. „Hvernig er hægt að draga ferningsrót af línustriki með hringfara einum?“ Vísindavefurinn, 4. október 2000, sótt 2. febrúar 2026, https://visindavefur.is/svar.php?id=968.
Stefán Ingi Valdimarsson. (2000, 4. október). Hvernig er hægt að draga ferningsrót af línustriki með hringfara einum? Vísindavefurinn. https://visindavefur.is/svar.php?id=968
Stefán Ingi Valdimarsson. „Hvernig er hægt að draga ferningsrót af línustriki með hringfara einum?“ Vísindavefurinn. 4. okt. 2000. Vefsíða. 2. feb. 2026. <https://visindavefur.is/svar.php?id=968>.
Þessi síða notar vafrakökur Nánari upplýsingar
Ég samþykki