Hvernig er hægt að nota Pýþagórasarreglu á praktískan hátt?

Nafn þitt

Netfang þitt

Netfang móttakanda

Ruslpóstvörn =

Svar

Hvernig er hægt að nota Pýþagórasarreglu á praktískan hátt?
Regla Pýþagórasar segir að í rétthyrndum þríhyrningi sé summan af lengd hvorrar skammhliðar um sig margfaldaðri með sjálfri sér jöfn lengd langhliðarinnar margfaldaðri með sjálfri sér. Tökum dæmi. Þríhyrningurinn á myndinni hér á eftir hefur hliðarnar a, b og c og hornið á móti hliðinni c er rétt eða 90°.

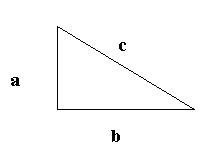
Um þennan þríhyrning gildir nú jafnan

a² + b² = c²

Ef hliðin a er 3 cm og hliðin b er 4 cm þá hlýtur hlið c að vera 5 cm vegna þess að

3² + 4² = 9 + 16 = 25 = 5²

Setjum sem svo að við séum að taka grunn að húsi sem er ferhyrnt, 8 m breitt og 10 m langt. Spurningin er þá hvernig við getum verið viss um að hafa grunninn hornréttan. Við gætum reynt að finna stóran vinkil, til dæmis vinkil sem væri með 4 metra arma. Það væri hins vegar mjög óhöndugt því ekki væri hægt að flytja vinkilinn í venjulegum bíl, hann væri alltof fyrirferðarmikill, og svo væri hann líka þungur og erfiður viðureignar.

En í staðinn fyrir vinkil dugir okkur að hafa nokkra hæla, band og málband. Við byrjum á að reka niður tvo hæla þar sem horn hússins eiga að vera og strengjum band á milli. Síðan mælum við þrjá metra eftir bandinu út frá öðrum hornhælnum og setjum niður lítinn hæl þar.

Þá tökum við 9m langt band, festum annan enda þess við þann hælinn sem er í horni hússins, mælum 4m eftir bandinu frá honum, merkjum þann stað á bandinu og festum hinn endann við litla hælinn.

Loks strekkjum við á bandinu frá báðum hælunum með því að toga í merkta punktinn. Þannig myndum við rétthyrndan þríhyrning og sú hlið þríhyrningsins sem er 4 metrar gefur okkur rétta stefnu húsveggsins, eins og sýnt er á myndinni hér á eftir.

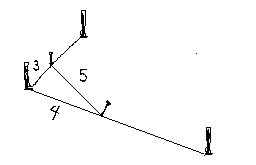
Þetta getum við svo endurtekið í hinum hornunum í húsinu til að tryggja að þau verði öll rétt.

Hér höfum við eitt dæmi um það hvernig hægt er að nota Pýþagórasarreglu á praktískan hátt. En reglan getur raunar komið að gagni á margan annan hátt. Hana má til dæmis nota til að reikna út fjarlægðir milli staða, sólarhæð og stærð hluta sem eru langt í burtu svo að eitthvað sé nefnt. Síðan er hún líka undirstaða undir ýmsar aðrar reglur og aðferðir sem notaðar eru í margs konar tilgangi....