Samsvörun:
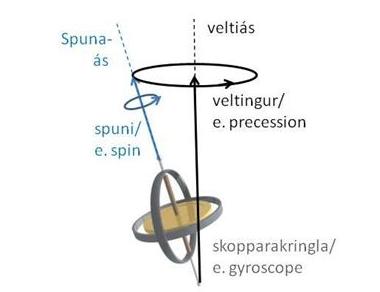
Til glöggvunar má líkja spuna efniseinda við snúningshreyfingu skopparakringlu (sjá mynd 1) að hluta. Skopparakringla byggir annars vegar á hringhreyfingu flatlaga efnishlutar (samanber hringlaga plötuna á mynd 1) um snúningsás. Hringhreyfingin kallast spuni og ásinn spunaás. Vegna þessarar spunahreyfingar hefur hluturinn ákveðinn hverfiþunga sem ræðst í senn af hraða hringhreyfingarinnar, massa hlutarins og stærð hans. Í samræmi við aflfræðilögmál eðlisfræðinnar veltist slík skopparakringla jafnframt á þann hátt að spunaás skopparakringlunnar snýst umhverfis ímyndaðan ás eins og sýnt er á myndinni. Sú hringhreyfing kallast veltingur (e. precession) og ásinn veltiás.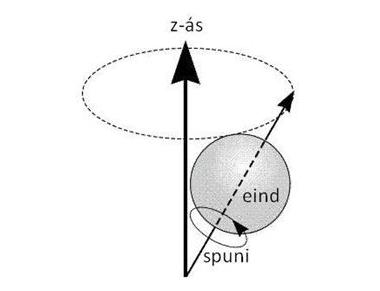
Nánar:
Efniseindir og eindir sem byggja kraftsvið hafa spuna og viðeigandi hverfiþunga sem er háður gerð eindanna (sjá mynd 2). Viðkomandi eindir eru af þrennum toga: i) öreindir (e. elementary particles), ii) sterkeindir (e. hadrons) og iii) atómkjarnar. Hverfiþungi (L) spunans ákvarðast af auðkennandi spunatölu (eða spunaskammtatölu) (s) samkvæmt skammtafræðinni: \(L=\sqrt{s(s+1)}\cdot \hbar\) þar sem \(\hbar=\frac{h}{2\Pi}\) og h er Plancks-fasti (\(h = 6,62606896(33)\cdot 10^{-34} Js\). Spunatölur geta tekið gildin núll og jákvæðar heiltölur (s = 0,1,2,3, ...) eða hálftölur (s = 1/2, 3/2, 5/2, ...). Til marks um spunatölur (s) má nefna s = 1/2 fyrir róteindir (p+) og rafeindir (e-), s = 1 fyrir ljóseindir og s = 5/2 fyrir atómkjarna álatómsins (27Al). Út frá þekktum spunatölum einda er auðvelt að reikna út hverfiþungann vegna spunans samkvæmt ofangreindri jöfnu. Hins vegar er ekki unnt að ákvarða afstöðu eða stefnu hverfiþungans. Þess í stað er einungis unnt að ákvarða afstæða stefnu hverfiþungans eftir ás (z-ás) sem samsvarar veltiásnum fyrir skopparakringluna (sjá myndir 1 og 2). Stærð hverfiþungans í stefnu þess áss (Lz) ákvarðast af líkingunni \[L_{z}=m_{s}\cdot \hbar\] þar sem (skammta)tölurnar ms geta tekið gildin ms = 0, \(\pm \)1, \(\pm \)2, \(\pm \)3, \(\pm \)4, ..., \(\pm \)s ef s eru 0 eða heiltölurms= \(\pm \)1/2, \(\pm \)3/2, \(\pm \)5/2, ..., \(\pm \)s ef s eru hálftölur.
.jpg)
- Hvað eru margar rafeindir á hverju hvolfi? eftir Ágúst Kvaran
- Hvað eru öreindir? eftir JGÞ
- Hvað er átt við með orðinu skammtafræði? eftir JGÞ
- Mynd 1 byggð á: Heidekolb's Blog. Sótt 12.12.2010.
- Mynd 2 byggð á: Curriculum Vitae - Principles of magnetic resonance imaging. Sótt 12.12.2010.
- Mynd 3 byggð á: Brooklyn College - Atomic structure. Sótt 12.12.2010.
