Hver er Andrew Wiles og hvernig tókst honum að sanna síðustu setningu Fermats?

Svar

Andrew John Wiles er bresk-bandarískur stærðfræðingur fæddur 1953. Hann er nú prófessor við Princeton-háskóla í Bandaríkjunum. Wiles er einn af þekktustu stærðfræðingum samtíðarinnar vegna sönnunar sinnar á síðustu setningu Fermats. Fyrir afrek hans aðlaði Bretadrottning Wiles árið 2000 en hann hefur hlotið margar aðrar viðurkenningar.

Síðasta setning Fermats er staðhæfingin að ef $n\geq 3$ þá eru ekki til jákvæðar heiltölur $x, y, z$ þannig að $$x^n+y^n=z^n.$$ Jöfnur þar sem krafist er að lausnirnar séu heiltölur eru kallaðar Díofantosarjöfnur eftir Díofantosi frá Alexandríu sem fæddur var um 200 e.Kr.

Staðhæfinguna hér að ofan mun franski stærðfræðingurinn Pierre de Fermat (1601-1665) hafa ritað á spássíuna á eintaki sínu af bók Díofantosar. Fermat skrifaði líka í bókina að hann hefði undursamlega sönnun á þessari staðhæfingu en því miður væri ekki pláss fyrir hana á spássíunni. Alla tíð síðan, í um 350 ár, hafa stærðfræðingar velt vöngum yfir þessari staðhæfingu. Það sem heillar er ekki síst hve einföld og auðskilin staðhæfingin er. Wiles segir frá því að hann hafi fyrst séð þessa staðhæfingu þegar hann var tíu ára og heillast strax.

Wiles lauk B.A.-prófi í stærðfræði frá Oxford-háskóla 1971 og flutti sig svo um set til Cambridge og lauk doktorsprófi þaðan. Þó hann hefði ávallt sjónar á síðustu setningu Fermats þá er þar ekki á vísan að róa og stærðfræðingur þarf á námsárum sínum og í upphafi ferils síns að velja sér verkefni þannig að líklegt sé að árangur náist. Wiles náði svo sannarlega góðum árangri í rannsóknum og var ráðinn til Princeton-háskóla 1982.

Á árunum 1985 og 1986 opnaðist svo ný leið til atlögu við síðustu setningu Fermats þegar sýnt var að sönnun á afmörkuðu tilfelli af tilgátu Tanayama og Shimura um sporgera ferla (e. elliptic curves) mundi leiða af sér sönnun á síðustu setningu Fermats. Wiles lagði þá öll önnur verkefni frá sér og einbeitti sér að síðustu setningu Fermats. Eftir átta ára yfirlegu steig Wiles fram í sviðsljósið og tilkynnti á ráðstefnu í Cambridge að hann hefði sannað síðustu setningu Fermats. Nú lögðust sérfræðingar yfir sönnunina og fljótlega fannst gloppa.


Bresk-bandaríski stærðfræðingurinn Andew Wiles. Á töflunni stendur síðasta setning Fermats.
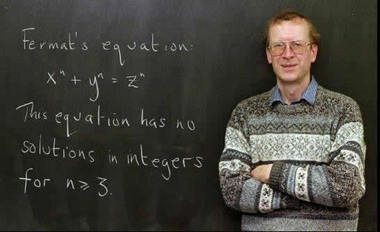
Eftir að hafa reynt að lagfæra sönnunina í heilt ár þá segir Wiles sjálfur svo frá að hann hafi verið að því kominn að gefast upp þegar hann fékk skyndilega hugljómun og sá hvernig hann gat lagfært sönnunina. Hann naut liðsinnis gamals nemanda síns, Richards Taylors, við að hnýta síðustu lausu endana og árið 1995 birtist svo í tímaritinu Annals of Mathematics rúmlega 100 síðna grein eftir Wiles og 20 síðna grein eftir Taylor og Wiles.

Þó síðasta setning Fermats hafi verið sönnuð þá er sögunni ekki enn lokið. Niðurstaðan sjálf skiptir sem slík litlu máli fyrir stærðfræði sem fræðigrein. Hið mikilvæga er sú fyrsta flokks stærðfræði sem hefur orðið til í glímunni við síðustu setningu Fermats. Heil fræðigrein, algebruleg talnafræði, er að verulegum hluta sprottin upp úr tilraunum manna við að sanna síðustu setningu Fermats. Sönnun Wiles markaði vissulega lokin á glímu mannkyns við síðustu setningu Fermats en hinar djúpu hugmyndir sem Wiles notaði í sönnun sinni munu um ókomin ár gefa af sér ný verkefni og nýjar niðurstöður í talnafræði. Ólíkt síðustu setningu Fermats þá má því miður búast við að þessi nýju verkefni verði aðeins skiljanleg sérfræðingum í talnafræði. Sönnunin sjálf mun líka verða til umfjöllunar og í ljósi sögunnar má gera ráð fyrir að hún verði stytt og einfölduð á ýmsan hátt en eflaust finnst ekki „einföld“ sönnun á síðustu setningu Fermats.

Frekara lesefni á Vísindavefnum:

• Hver var síðasta setning Fermats? eftir Gunnar Þór Magnússon
• Hvernig er sagan af því þegar Perelman leysti Poincaré-tilgátuna? eftir Robert Magnus og Heiðu Maríu Sigurðardóttur
• Getið þið sannað Goldbach-tilgátuna? eftir Gunnar Þór Magnússon
• Hefur tilgáta Riemanns verið sönnuð? eftir Ragnar Sigurðsson
• Hver var Vilhjálmur Ögmundsson og hvert var hans framlag til stærðfræðinnar? eftir Kristínu Bjarnadóttur
• Hver var Andrei Kolmogorov og hvert var framlag hans til stærðfræðinnar? eftir Hermann Þórisson
• Hver var Gaston Julia? eftir Gunnar Þór Magnússon

Myndir:

• Wikipedia.com - Pierre de Fermat. Sótt 27.1.2011.
• Wikipedia.com - Andrew John Wiles. Sótt 27.1.2011.