Hvaða stærðfræði liggur að baki gervitauganetum og mállíkönum?Stærðfræðilegur grunnur gervitauganeta Hugtakið gervigreind er í dag aðallega notað um tækni sem byggir á svokölluðum gervitauganetum (e. Artificial Neural Networks, ANNs) og hagnýtingu þeirra. Þrátt fyrir að slík net sæki innblástur í líffræðileg tauganet þá eru þau í grunninn stærðfræðileg líkön. Hæfni þeirra til að læra af gögnum byggir á samspili nokkurra kjarnagreina stærðfræðinnar. Þær helstu eru línuleg algebra, stærðfræðigreining, og bestun. Til eru margar mismunandi gerðir tauganeta en þau byggja flest á þessum kjarnagreinum. Tauganetin eiga það einnig flest sameiginlegt að þau samanstanda af mörgum lögum (e. layer) þar sem hvert lag inniheldur margar einingar, svokallaðar gervitaugafrumur. Lögin eru svo tengd saman og hver tenging hefur venjulega svonefnda vogtölu (e. weight) sem lýsir því hversu mikil áhrif ein gervitaugafruma getur haft á aðrar. Almennt eru vogtölur (og aðrar tölur sem hægt er að uppfæra í þjálfunarferlinu) kallaðar stikar (e. parameters). Þegar gervitauganet framkvæmir útreikninga er yfirleitt byrjað á inntakslaginu en virkjun þess endurspeglar einhverjar breytur. Til einföldunar er til dæmis hægt að hugsa sér að sérhver díll (e. pixel) á stafrænni mynd sé gervitaugafruma og gildi dílsins er virkjunargildi hennar. Þessi virkjunargildi eru svo notuð til að reikna virkjunargildin í næsta lagi og svo framvegis, þangað til komið er að úttakslaginu en þar mætti mögulega finna gervitaugafrumur sem endurspegla flokkun þar sem stök fruma myndi til dæmis segja til um hvort það sé köttur á myndinni eða ekki. Hér fyrir neðan er farið stuttlega yfir það hvernig kjarnagreinarnar sem nefndar voru hér að ofan tengjast gervitauganetum.
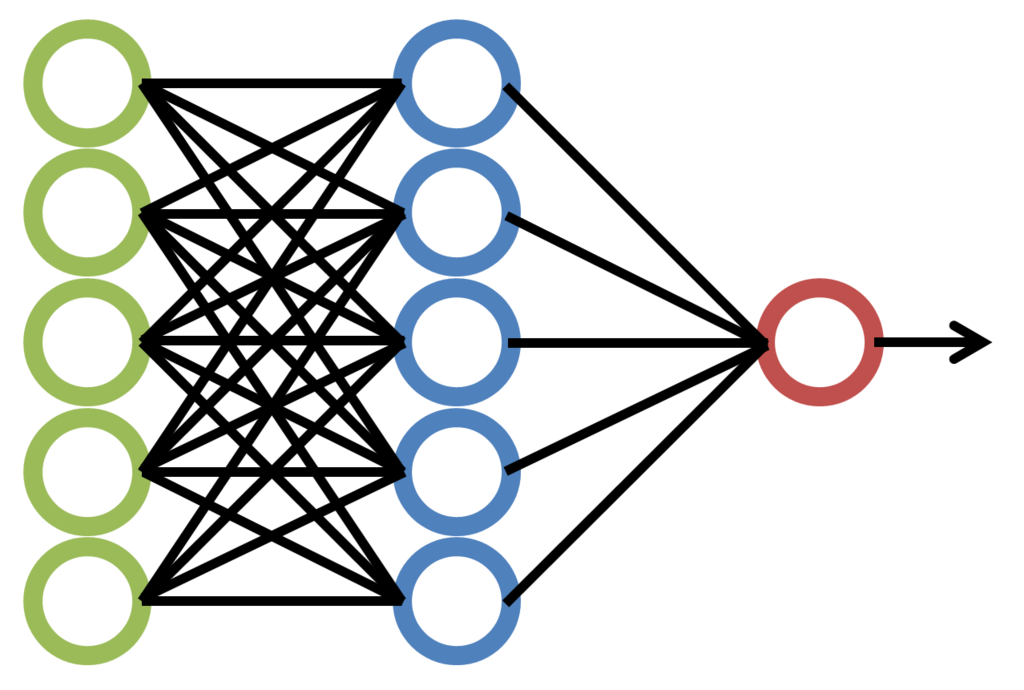
Skýringarmynd af einföldu þriggja laga gervitauganeti. Grænu gervitaugafrumurnar tákna inntakslagið, þær bláu reikna virkjunargildin sem koma vegna inntaks frá þeim grænu og rauða gervitaugafruman er úttakslagið.
- Framsetning gagna: Inntaksgögn fyrir tauganet, svo sem myndir, texti eða töflugögn, eru sett fram sem vigrar, fylki eða þinir (e. tensor, margvíð fylki). Til dæmis er hægt að tákna svarthvíta mynd sem fylki þar sem hvert stak táknar birtustig eins díls.
- Stikar netsins: „Þekking“ netsins er geymd í stikum þess. Stikarnir eru til dæmis í formi vogtalna sem lýsa styrkleika tenginga tauganetsins. Vogtölur eru yfirleitt geymdar í fylkjum (W).
- Útreikningur: Grundvallaraðgerð innan einnar gervitaugafrumu er línuleg vörpun sem fylgt er eftir með ólínulegu virkjunarfalli. Þetta er sett fram sem fylkjamargfeldi inntaksvigurs (x) og vogtölufylkis (W), að viðbættum vigri (b) sem inniheldur svonefnt bjagagildi. Jafnan fyrir úttak lagsins, áður en virkjunarfalli er beitt, er: $$z = W \cdot x + b$$ Þessi aðgerð er reikningslega hagkvæm, sérstaklega með nútíma vélbúnaði á borð við skjákort (GPU), sem eru sérhönnuð fyrir fylkjamargföldun.
- Tapfall: Tapfall (e. loss function), L, mælir muninn á spá netsins og óskgildi (e. target value). Markmið þjálfunar er að finna það mengi vogtalna og stika sem lágmarkar þetta fall.
- Stiglar: Til að skilja hvernig stilla skal hvern stika til að minnka tapið þurfum við að reikna hlutafleiðu tapfallsins með tilliti til stikanna, til dæmis væri hún táknuð sem $\frac{\partial L}{\partial W}$ þegar við einskorðum okkur við vogtölur frá einu lagi yfir annað. Þessi afleiða, sem nefnist stigull (e. gradient), segir til um stefnu og stærð brattasta vaxtarhraða tapfallsins.
- Afturbreiðsla (e. backpropagation): Tauganet samanstanda af mörgum lögum. Keðjureglan úr stærðfræðigreiningu er hornsteinn afturbreiðslunnar (e. backpropagation), sem er reiknirit til að reikna stigul tapsins með tilliti til allra stika í netinu á skilvirkan hátt, allt frá úttakslaginu og aftur til inntakslagsins. Þessi afturbreiðsla skekkjunnar er nauðsynleg til að þjálfa djúp tauganet.
- Stigulsaðferð (e. Gradient Descent): Þetta bestunarreiknirit liggur til grundvallar allri þjálfun tauganeta. Uppfærsluregluna má setja fram á þessa vegu: $$W = W - \eta \cdot \frac{\partial L}{\partial W}$$ Hér er η (eta) lærdómshraðinn (e. learning rate) sem er yfirstiki (e. hyperparameter) sem stýrir skrefastærðinni.
- Betri bestunaraðferðir: Þróaðar hafa verið aðrar aðferðir á borð við slembna stigulsaðferð (e. Stochastic Gradient Descent), Adam, RMSprop og Adagrad. Þessar aðferðir aðlaga lærdómshraðann á meðan á þjálfun stendur og nýta sér hugtök eins og skriðþunga (e. momentum) til að flakka um hið flókna og margvíða „taplandslag“ á skilvirkari hátt. Þetta leiðir til skilvirkari þjálfunar og meiri nákvæmni.
- Upphafsstilling og reglun: Stikar netsins eru oft upphafsstilltir með slembigildum úr ákveðnum líkindadreifingum til að tryggja að virkni gervitaugafrumanna springi ekki eða dvíni of snemma. Tölfræðilegar aðferðir eins og brottfall (e. dropout) og L1/L2 reglun (e. regularization) eru notaðar til að koma í veg fyrir ofþjálfun, sem gerist þegar líkan stendur sig vel á þjálfunargögnum en illa á gögnum sem það var ekki þjálfað á.
- Yfirlitsmynd: Free Images - PxHere. (Sótt 22.09.2025).
- File:NeuralNetwork.png - Wikimedia Commons. (Sótt 22.09.2025).

