Sólin
Rís 10:17 • sest 16:10
Tunglið
Rís 21:40 • Sest 15:54
Flóð
Árdegis: 10:12 • Síðdegis: 22:46
Fjara
Árdegis: 03:46 • Síðdegis: 16:36
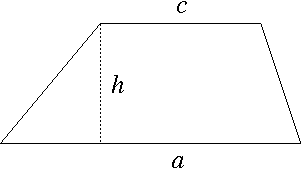
Það er ekki erfitt að leiða þessa formúlu út ef við kunnum að reikna út flatarmál þríhyrninga og samsíðunga. Við skiptum trapisunni okkar upp í samsíðung með hæð h og hliðarlengd c, og þríhyrning með hæð h og grunnlínu a-c, eins og er gert á myndinni hér að neðan.
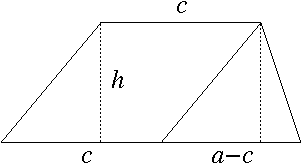
Nú reiknum við að flatarmál samsíðungsins er jafnt h∙c og flatarmál þríhyrningsins er jafnt h∙(a-c)/2. Þegar við leggjum þetta saman fáum við að flatarmál trapisunnar er jafnt \[F=hc+\frac{h(a-c)}{2}=\frac{h(a+c)}{2}\] Við getum einnig reiknað flatarmál trapisu ef við þekkjum allar hliðarlengdir hennar en ekki hæðina, með svipaðri reglu og gildir fyrir þríhyrninga. Þetta er þó aðeins hægt ef samsíða hliðar trapisunnar eru mislangar. Formúlan fyrir flatarmálinu verður þá flóknari og við látum nægja að birta hana hér, en leiðum hana ekki út. Skoðum trapisu með hliðar a, b, c og d eins og hér að neðan, þar sem hliðarnar a og c eru samsíða og a er lengri hliðin.
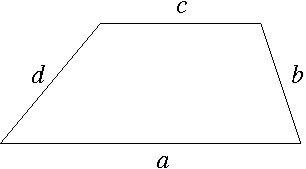
Ef við látum s = (a + b + c + d)/2 vera hálft ummál trapisunnar, þá er flatarmál hennar jafnt \[F=\frac{a+c}{a-c}\sqrt{(s-c)(s-a)(s-c-b)(s-c-d)}\] Tengt efni á Vísindavefnum:
- Hvernig má finna flatarmál þríhyrninga ef allar hliðarlengdir eru þekktar en engin horn? eftir Einar Örn Þorvaldsson.
- Hvernig er trapisa skilgreind? eftir ÞV.
- Hvernig er regla Pýþagórasar sönnuð? eftir Gunnar Þór Magnússon.
