Hvað er 1.000.000.000.000.000 í öðru veldi?Stundum er talað um reikniaðgerðina margföldun sem „endurtekna samlagningu“. Það er vegna þess að í sinni einföldustu mynd er margföldun notuð til að einfalda rithátt þegar sama talan er lögð við sjálfa sig aftur og aftur. Í stað þess að skrifa til dæmis \[\underbrace{8+8+8+8+8}_{\text{5 sinnum}}\] er skrifað \[5 \cdot 8.\] Á sama hátt mætti segja að svokölluð veldi séu „endurtekin margföldun“. Þau eru sem sagt notuð til að einfalda rithátt þegar sama talan er margfölduð við sjálfa sig aftur og aftur. Í stað þess að skrifa til dæmis \[\underbrace{7 \cdot 7 \cdot 7 \cdot 7}_{\text{4 sinnum}}\] er skrifað \[7^4,\] og þessi tala kallast „sjö í fjórða veldi“. Í stað þess að skrifa \[\underbrace{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2}_{\text{6 sinnum}}\] er á sama hátt skrifað \[2^6,\] og þessi tala kallast „tveir í sjötta veldi“. Ef $x$ er einhver tala (rauntala) og $n$ er einhver jákvæð heiltala, þá er almennt hægt að skilgreina veldið $x^n$ svona: \[x^n = \underbrace{x \cdot x \cdot x \cdot \ldots \cdot x}_{\text{$n$ sinnum}}.\] Með þessu er átt við að talan $x^n$ fæst með því að margfalda töluna $x$ við sjálfa sig $n$ sinnum, eða með því að margfalda saman $n$ eintök af tölunni $x$. Hægt er að útvíkka skilgreiningu veldisins $x^n$ þannig að talan $n$ geti líka verið $0$ eða neikvæð heiltala. Áður en það er gert skulum við líta á eftirfarandi töflu:
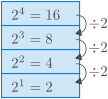
Vert er að veita því athygli að til að fá næstu tölu fyrir ofan í töflunni þarf að margfalda með $2$, en til að fá næstu tölu fyrir neðan þarf að deila með $2$. Ef byrjað er efst í töflunni, þá fæst næsta veldi fyrir neðan alltaf með því að deila með $2$. Með því að fylgja þessari reglu sjáum við hvernig eðlilegt er að bæta $2^0$, $2^{-1}$, $2^{-2}$, og svo framvegis, inn í töfluna:

Með þessari hugsun fæst að $2^0=1$. Ef bornar eru saman efsta og neðsta línan, næstefsta og næstneðsta línan, og svo framvegis, sést jafnframt að $$\begin{align*} &2^{-4} = \frac1{16} = \frac1{2^4}, \quad\quad 2^{-3}=\frac18=\frac1{2^3}, \quad\quad \text{o.s.frv.} \end{align*}$$ Með öðrum orðum gildir fyrir sérhverja neikvæða heiltölu $-n$ að \[2^{-n} = \frac1{2^n}.\] Ef prófað er að setja aðra tölu í stað $2$ í töflunni að ofan fæst nákvæmlega sama mynstrið. Þess vegna er eðlilegt að skilgreina almennt \[x^0 = 1 \quad\text{og}\quad x^{-n} = \frac1{x^n},\] þar sem $x$ getur verið hvaða tala sem er önnur en $0$. Ástæðan fyrir því að $x$ getur ekki verið $0$ er að ef $0$ er notað í stað $2$ í töflunni að ofan, þá þarf alltaf að deila með $0$ til að fá næstu tölu fyrir neðan, sem er ekki skilgreind aðgerð í stærðfræði. Um veldi gilda eftirfarandi fimm reiknireglur, sem oft eru kallaðar veldareglurnar:
- $x^m \cdot x^n = x^{m+n}$.
- $\frac{x^m}{x^n} = x^{m-n}$ ef $x \neq 0$.
- $(x^m)^n = x^{m \cdot n}$.
- $(x \cdot y)^m = x^m \cdot y^m$.
- $(\frac{x}y)^m = \frac{x^m}{y^m}$ ef $y \neq 0$.
Hvað er 1.000.000.000.000.000 í öðru veldi?Til að svara henni er einfaldast að taka eftir því að talan 1.000.000.000.000.000 er ekkert annað en $10^{15}$, því hún hefur fimmtán núll. Þá er hægur vandi að hefja töluna í annað veldi með því að nota þriðju veldaregluna að ofan: \[(10^{15})^2 = 10^{15 \cdot 2} = 10^{30}.\] Ef talan $10^{30}$ er skrifuð á hefðbundnu formi byrjar hún á einum og þar á eftir fylgja þrjátíu núll, sem sagt \[1.000.000.000.000.000.000.000.000.000.000.\] Þetta er gríðarstór tala; til dæmis er hún hálfur massi sólarinnar í kílóum talið.
Þetta svar var upprunalega skrifað árið 2011, þegar höfundur var starfsmaður Vísindavefsins.
