Hver bjó til eða fann upp talnagrindina?

Nafn þitt

Netfang þitt

Netfang móttakanda

Ruslpóstvörn =

Svar

Hver bjó til eða fann upp talnagrindina?
Talnagrind var þekkt í mörgum fornum þjóðfélögum. Ógerningur er að vita hver bjó hana fyrstur til. Vitað er um að talnagrind hafi verið notuð í Mesópótamíu um 2500 f.Kr., meðal Persa um 600 f.Kr., og bæði meðal Grikkja og Rómverja á blómaskeiðum menningar þeirra á fyrstu öldum f.Kr. Notkun talnagrindarinnar breiddist út um Evrópu og til Kína og Japans. Þar varð talnagrindin helsta tækið til útreikninga mörgum öldum áður en tekin var upp talnaritun í sætiskerfi með grunntölunni tíu, indó-arabísk talnaritun. Myndin hér á eftir af kínverskri talnagrind úr bókinni Suan Fa Thung Tsung (Kerfisbundið fræðirit um reikning) eftir Cheng Ta-Wei frá árinu 1593.

Kínversk talnagrind, suanpan, og japönsk talnagrind, soroban, eru gerðar úr ramma með rimlum. Litlar kúlur eða perlur eru festar á rimlana og hægt að renna þeim til. Rimlarnir tákna sæti þannig að gildi einnar kúlu er tífalt gildi kúlu á rimli hægra megin við hana.

Rammanum er skipt í tvennt. Öðrum megin við skiptistöngina eru fimm kúlur sem tákna einfalt gildi en hinum megin eru tvær kúlur sem tákna fimmfalt gildi á suanpan, en ein kúla á soroban.

Kínverska talnagrindin á myndinni hér á eftir hefur ellefu rimla. Rimillinn lengst til hægri táknar tíundu hluta, sá næsti einingu, þá koma tugur, hundrað, þúsund ... Aðeins eru taldar kúlurnar sem rennt hefur verið að skiptistönginni. Myndin sýnir 123 456 789 eða eitt hundrað tuttugu og þrjár milljónir, fjögur hundruð fimmtíu og sex þúsund, sjö hundruð áttatíu og níu.

Talnagrindin var í virkri notkun í Rússlandi, Kína og Japan í verslunum og skrifstofum langt fram á tuttugustu öld. Kennt var á talnagrindina í skólum í Sovétríkjunum fram yfir 1990. Árið 1946 fór fram keppni milli japansks skrifstofumanns sem notaði talnagrind og bandarísks ofursta sem notaði rafknúna reiknivél. Talnagrindin hafði sigur í öllum aðgerðum nema margföldun, og færri villur voru gerðar með henni. Líklegt er að vasareiknar hafi þó að miklu leyti tekið yfir síðustu áratugina.

Heimildir:

• Boyer, Carl, og Merzbach, Uta (1989). A history of mathematics. Önnur útgáfa. New York: John Wiley and Sons.
• Needham, Joseph (1954, 1959). Science and civilisation in China. 3. bindi. Cambridge: Cambridge University Press.
• Abacus - Wikipedia. (Sótt 12.09.2017).

Myndir:

• A brief history of numbers and statistics with cytometric applications - Watson - 2001 - Cytometry Part A - Wiley Online Library. (Sótt 12.09.2017).
• File:2017 Ono soroban.jpeg - Wikimedia Commons. (Sótt 12.09.2017).
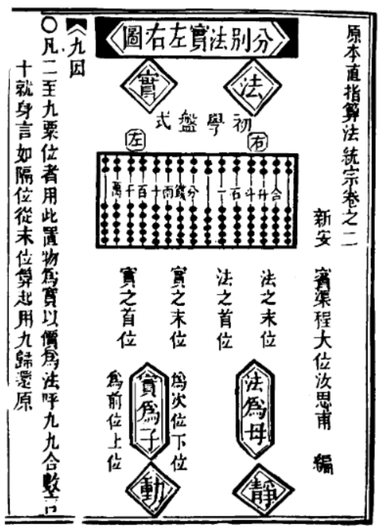
• Mynd af kínverskri talnagrind: Science and Civilisation in China, 3. bindi. eftir Joseph Needham. Cambridge University Press, 1959.

...