Hvernig sannið þið að hlutfall ummáls hrings og þvermáls sé fasti óháður geisla hringsins?

Nafn þitt

Netfang þitt

Netfang móttakanda

Ruslpóstvörn =

Svar

Hvernig sannið þið að hlutfall ummáls hrings og þvermáls sé fasti óháður geisla hringsins?
Í flatarmyndafræði er sagt að tvær flatarmyndir séu einslaga ef sama hlutfallið er milli sérhverrar lengdar í annarri myndinni og tilsvarandi lengdar í hinni. Til dæmis eru fimmhyrningarnir tveir á myndinni að neðan einslaga, því ef reiknuð eru hlutföllin milli tilsvarandi lengda í þeim fæst:

\[\frac42 = 2, \quad \frac42 = 2, \quad \frac63=2, \quad \frac{10}5=2 \quad\text{og}\quad \frac84=2.\]

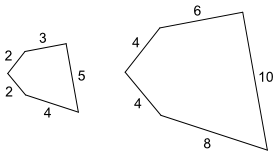
Ef fimmhyrningarnir eru skoðaðir nánar sést að þeir eru alveg eins í laginu, nema hvað að þeir eru misstórir. Þess vegna er hægt að hugsa sér að hægri fimmhyrningurinn sé stækkuð útgáfa af þeim vinstri. Þetta gildir almennt um tvær flatarmyndir sem eru einslaga.

Með lýsinguna úr síðustu efnisgrein í huga er auðvelt að sjá að tveir ólíkir hringir eru alltaf einslaga. Á þessari staðreynd byggist líklega einfaldasta sönnunin á að hlutfallið milli ummáls og þvermáls hrings sé fasti, og nú verður hún sett fram.

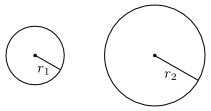
Segjum að við höfum tvo ólíka hringi sem hafa geisla $r_1$ og $r_2$. Köllum þvermál hringjanna $þ_1$ og $þ_2$ og ummál þeirra $U_1$ og $U_2$. Þar sem hringirnir eru einslaga vitum við að sama hlutfallið er milli sérhverrar lengdar í öðrum hringnum og tilsvarandi lengdar í hinum. Það þýðir að sama hlutfall er milli ummála hringjanna annars vegar og þvermála þeirra hins vegar, það er

\[\frac{U_1}{U_2} = \frac{þ_1}{þ_2}.\]

Margföldum nú báðar hliðar þessarar jöfnu með stærðinni $\frac{U_2}{þ_1}$:

\[\frac{U_2}{þ_1} \cdot \frac{U_1}{U_2} = \frac{U_2}{þ_1} \cdot \frac{þ_1}{þ_2}.\]

Nú er hægt að stytta $U_2$ út í vinstri hlið jöfnunnar og $þ_1$ í hægri hlið hennar. Þannig fæst:

\[\frac{U_1}{þ_1} = \frac{U_2}{þ_2}.\]

Þessi jafna segir að ef reiknað er hlutfallið milli ummáls og þvermáls fyrri hringsins, þá fæst það sama út og þegar reiknað er hlutfallið milli ummáls og þvermáls seinni hringsins. Við höfum þá sýnt að hlutfallið milli ummáls og þvermáls hrings er fasti, sem er einmitt það sem við vildum sanna.

Mikilvægi staðhæfingarinnar sem við vorum að sanna felst í því að hún gerir okkur kleift að skilgreina töluna $\pi$ sem hlutfallið milli ummáls og þvermáls hrings. Þessi skilgreining væri auðvitað tóm steypa ef hlutfallið væri ekki það sama í öllum hringjum. Nánar má lesa um töluna $\pi$ í svari Eggerts Briem við spurningunni Hverjir „fundu upp“ π (pí)? og svari Hrannars Baldurssonar og Þorsteins Vilhjálmssonar við spurningunni Hvað hefur talan pí marga aukastafi og hverjir eru þeir?

Upprunalega hljóðaði spurningin svona:

Vinsamlegast leggið fram sönnun þess að hlutfall ummáls hrings og þvermáls sé fasti óháður geisla hringsins?

...