 Apollóníos fæddist í Perga á strönd Litlu-Asíu rétt hjá þar sem nú er ferðamannaborgin Antalya í Tyrklandi. Lítið er vitað um líf hans, æsku eða uppvöxt, en rit hans höfðu mikil áhrif á stærðfræðinga síðari tíma, svo sem Ptólemaíos, Kepler, Galíleó, Newton og Descartes, svo og á þróun íslamskrar rúmfræði á miðöldum. Vitað er að Apollóníos nam stærðfræði í hinu mikla menntasetri í Alexandríu við ósa Nílar þar sem nú er Egyptaland. Kennarar hans voru eftirmenn Evklíðs og Apollóníos kenndi þar sjálfur síðar. Hann dvaldist einnig í Pergamon, nú Bergama í Tyrklandi, borg sem gekk næst Alexandríu á vísindasviðinu með miklu bókasafni og öflugu skólastarfi.
Meginverk Apollóníosar var Keilusnið (e. Conics), rit sem skiptist í átta bækur. Aðeins fjórar fyrstu bækurnar hafa varðveist á frummálinu grísku en fyrstu sjö bækurnar geymdust í arabískri þýðingu.
Samkvæmt skilgreiningu eru keilusnið skurðferlarnir sem myndast þegar sléttur flötur sker yfirborð keilu. Til þeirra teljast hringur, sporbaugur (e. ellipse), fleygbogi (e. parabola) og breiðbogi (e. hyperbola). Í formála sínum að Keilusniðum útskýrir Apollóníos hvað varð til þess að hann ritaði þetta fræga verk:
Apollóníos fæddist í Perga á strönd Litlu-Asíu rétt hjá þar sem nú er ferðamannaborgin Antalya í Tyrklandi. Lítið er vitað um líf hans, æsku eða uppvöxt, en rit hans höfðu mikil áhrif á stærðfræðinga síðari tíma, svo sem Ptólemaíos, Kepler, Galíleó, Newton og Descartes, svo og á þróun íslamskrar rúmfræði á miðöldum. Vitað er að Apollóníos nam stærðfræði í hinu mikla menntasetri í Alexandríu við ósa Nílar þar sem nú er Egyptaland. Kennarar hans voru eftirmenn Evklíðs og Apollóníos kenndi þar sjálfur síðar. Hann dvaldist einnig í Pergamon, nú Bergama í Tyrklandi, borg sem gekk næst Alexandríu á vísindasviðinu með miklu bókasafni og öflugu skólastarfi.
Meginverk Apollóníosar var Keilusnið (e. Conics), rit sem skiptist í átta bækur. Aðeins fjórar fyrstu bækurnar hafa varðveist á frummálinu grísku en fyrstu sjö bækurnar geymdust í arabískri þýðingu.
Samkvæmt skilgreiningu eru keilusnið skurðferlarnir sem myndast þegar sléttur flötur sker yfirborð keilu. Til þeirra teljast hringur, sporbaugur (e. ellipse), fleygbogi (e. parabola) og breiðbogi (e. hyperbola). Í formála sínum að Keilusniðum útskýrir Apollóníos hvað varð til þess að hann ritaði þetta fræga verk:Ég fór að fást við þetta efni að beiðni Nákratesar rúmfræðings þegar hann kom til Alexandríu og dvaldist hjá mér, og þegar ég hafði unnið verkið sem fyllti átta bækur fékk ég honum þær í of miklum flýti af því að hann var að sigla á braut; þær höfðu því ekki verið vandlega yfirfarnar; satt að segja hafði ég skráð niður allt sem mér kom í hug og geymt yfirlesturinn þar til í lokin.
... mestu og fegurstu setningarnar eru nýjar og það var þegar ég uppgötvaði þær sem ég sá að Evklíð hafði ekki unnið til fulls sameinaðar reglur um leg (e. locus) með tilliti til þriggja og fjögurra lína ... þær var ekki unnt að fullgera nema með hjálp setninganna sem ég fann.Fimmta, sjötta og sjöunda bók Keilusniða eru mjög frumlegar. Þar ræðir Apollóníos þverla (hornréttar línur, e. normals) á keilusnið og sýnir fram á hve marga þverla megi draga frá gefnum punkti. Af þessum bókum þykir fimmta bókin merkilegust vegna þverlanna. Ritið Keilusnið þykir snilldarverk, sem fáir hafa kynnt sér til hlítar. Efni þess er mjög samanþjappað og þar er að finna 387 sannaðar reglur. Að hluta til eru reglurnar svo margar þar sem Grikkir höfðu það fyrir sið að sanna öll sértilvik sérstaklega en einnig er ritið torlesið vegna skorts á táknmáli. Pappos var síðasti rúmfræðingur Forngrikkja sem lét eitthvað að sér kveða. Pappos segir frá sex öðrum verkum Appolóníusar en aðeins eitt þeirra, Hlutfallaskurður, hefur varðveist í arabískri þýðingu.
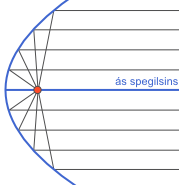 Þótt verk Apollóníosar séu glötuð má leiða líkur að því að efni þeirra hafi varðveist í íslömskum ritum. Meðal rita sem fornir höfundar vitna til er Um brennandi spegilinn, þar sem hann mun meðal annars hafa ritað um eiginleika spegils í fleygbogafleti (e. paraboloid, sjá mynd hér til hliðar). Spegill í fleygbogafleti safnar geislum, sem koma inn samsíða ás spegilsins, í einn punkt, brennipunktinn (e. focus). Öfugt gildir einnig að geislar frá ljósgjafa sem komið er fyrir í brennipunktinum kastast af speglinum samsíða ás hans. Eiginleiki þessi er notaður í ljóskösturum, við merkjasendingar ýmiss konar og í móttökutækjum.
Rannsóknir Apollóníosar á keilusniðum voru rúmfræðilegar athuganir á hinum tilteknu skurðferlum. Við þær var engu bætt allt frá dögum Papposar, sem kann að hafa verið síðastur manna til að skilja rit Apollóníusar þar til komið var fram á daga Keplers, Galíleós, Newtons og Descartes. Þá nýttust kenningar Apollóníosar vel, til dæmis þegar Kepler sýndi fram á að brautir reikistjarnanna eru sporbaugar og einnig í athugunum á fleygbogaferlum fallbyssukúlna og annarra kasthluta. Descartes og eftirmenn hans sköpuðu umgjörðina með því að færa rúmfræðina inn í hnitakerfi en það gerði mönnum kleift að beita algebrunni, hinu öfluga táknmáli stærðfræðinnar. Raunar er talið að aðferðir Appolóníusar hafa ekki verið ólíkar vinnu í hnitakerfi og að hjá honum megi finna vísi að verki Descartes, hnitarúmfræðinni, 1800 árum síðar.
Verk Apollóníosar um keilusnið teljast til stærðfræði en niðurstöður hans hafa engu að síður verið mikið notaðar í stjörnufræði og eðlisfræði; slíkt notagildi á einmitt við um margar fullyrðingar stærðfræðinnar. En auk þessara stærðfræðilegu viðfangsefna fékkst Apollóníos einnig við eiginlega stjörnufræði eins og hún var iðkuð á þeim tíma. Verk hans um þetta hafa hins vegar ekki varðveist nema að því leyti að talið er þau hafi haft veruleg áhrif á Ptólemaíos sem var tvímælalaust mesti stjarnfræðingur forngríska skeiðsins og skrifaði heildstæð rit um stjörnufræði sem hafa varðveist fram á þennan dag.
Keilusniðin búa yfir heillandi fegurð, bæði sjónrænni í sveigjum ferlanna og í einfaldri framsetningu sem stærðfræðingar kunna vel að meta. Mikið samræmi er til dæmis með jöfnum þeirra í svonefndum pólhnitum. Sama á við um einföldustu jöfnur þeirra í kartesísku hnitakerfi sem eru þekktari:
Þótt verk Apollóníosar séu glötuð má leiða líkur að því að efni þeirra hafi varðveist í íslömskum ritum. Meðal rita sem fornir höfundar vitna til er Um brennandi spegilinn, þar sem hann mun meðal annars hafa ritað um eiginleika spegils í fleygbogafleti (e. paraboloid, sjá mynd hér til hliðar). Spegill í fleygbogafleti safnar geislum, sem koma inn samsíða ás spegilsins, í einn punkt, brennipunktinn (e. focus). Öfugt gildir einnig að geislar frá ljósgjafa sem komið er fyrir í brennipunktinum kastast af speglinum samsíða ás hans. Eiginleiki þessi er notaður í ljóskösturum, við merkjasendingar ýmiss konar og í móttökutækjum.
Rannsóknir Apollóníosar á keilusniðum voru rúmfræðilegar athuganir á hinum tilteknu skurðferlum. Við þær var engu bætt allt frá dögum Papposar, sem kann að hafa verið síðastur manna til að skilja rit Apollóníusar þar til komið var fram á daga Keplers, Galíleós, Newtons og Descartes. Þá nýttust kenningar Apollóníosar vel, til dæmis þegar Kepler sýndi fram á að brautir reikistjarnanna eru sporbaugar og einnig í athugunum á fleygbogaferlum fallbyssukúlna og annarra kasthluta. Descartes og eftirmenn hans sköpuðu umgjörðina með því að færa rúmfræðina inn í hnitakerfi en það gerði mönnum kleift að beita algebrunni, hinu öfluga táknmáli stærðfræðinnar. Raunar er talið að aðferðir Appolóníusar hafa ekki verið ólíkar vinnu í hnitakerfi og að hjá honum megi finna vísi að verki Descartes, hnitarúmfræðinni, 1800 árum síðar.
Verk Apollóníosar um keilusnið teljast til stærðfræði en niðurstöður hans hafa engu að síður verið mikið notaðar í stjörnufræði og eðlisfræði; slíkt notagildi á einmitt við um margar fullyrðingar stærðfræðinnar. En auk þessara stærðfræðilegu viðfangsefna fékkst Apollóníos einnig við eiginlega stjörnufræði eins og hún var iðkuð á þeim tíma. Verk hans um þetta hafa hins vegar ekki varðveist nema að því leyti að talið er þau hafi haft veruleg áhrif á Ptólemaíos sem var tvímælalaust mesti stjarnfræðingur forngríska skeiðsins og skrifaði heildstæð rit um stjörnufræði sem hafa varðveist fram á þennan dag.
Keilusniðin búa yfir heillandi fegurð, bæði sjónrænni í sveigjum ferlanna og í einfaldri framsetningu sem stærðfræðingar kunna vel að meta. Mikið samræmi er til dæmis með jöfnum þeirra í svonefndum pólhnitum. Sama á við um einföldustu jöfnur þeirra í kartesísku hnitakerfi sem eru þekktari:
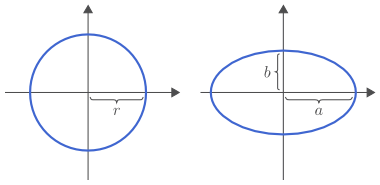
Vinstri myndin sýnir hring með geisla $r$. Hægri myndin sýnir sporbaug með hálfan langás $a$ og hálfan skammás $b$.
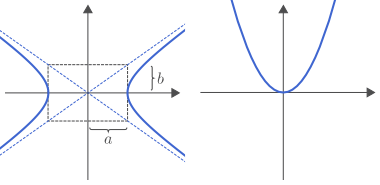
Blái ferillinn á vinstri myndinni er breiðbogi með hálfan meginás $a$ og hálfan þverás $b$. Ferillinn leggst að bláu punktalínunum, sem eru aðfellur breiðbogans. Hægri myndin sýnir fleygboga.
- Þorsteinn Vilhjálmsson, 1986-1987. Heimsmynd á hverfanda hveli, I-II. Sagt frá heimssýn vísindanna frá öndverðu fram yfir daga Newtons. Reykjavík: Mál og menning.
- Appolonius of Perga. Britannica, Academic Edition. http://www.britannica.com/EBchecked/topic/30058/Apollonius-of-Perga.
- Appolonius of Perga. Vefur St. Andrews-háskóla í Skotlandi. http://www-history.mcs.st-and.ac.uk/Biographies/Apollonius.html.
- Appolonius of Perga. Wikipedia, the free encyclopedia. https://secure.wikimedia.org/wikipedia/en/wiki/Apollonius_of_Perga.
- Boyer, C.B. og Merzbach, U.C. (1991). A history of mathematics. Önnur útgáfa. New York: John Wiley and Sons, Inc.
- Jón Þorvarðarson (2005). Og ég skal hreyfa jörðina. Forngrísku stærðfræðingarnir og áhrif þeirra. Reykjavík: STÆ, ehf.
- The Internet Encyclopedia of Science - Apollonius of Perga. Sótt 28.2.2011.
- Wolfram MathWorld. Mynd íslenskuð af ritstjórn. Sótt 28.2.2011.
- Aðrar myndir: EBG.
